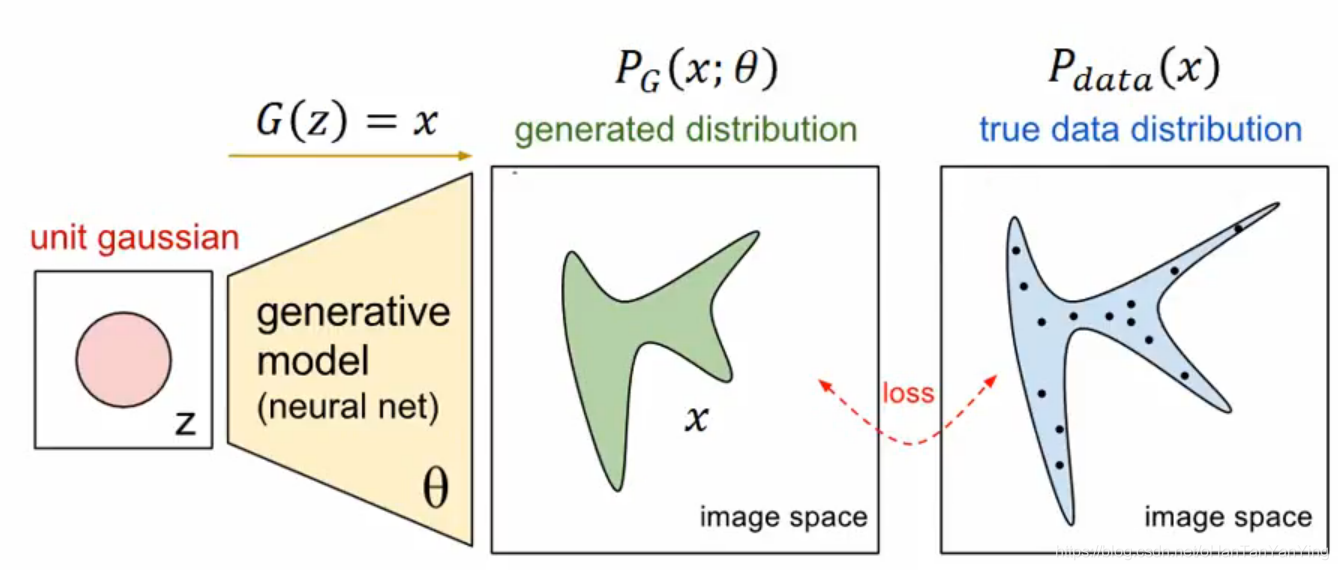
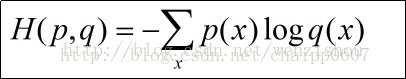GAN生成对抗式神经网络实际操作
上一篇文章我们强力推导了GAN的数学公式,它就是:
$$
V = E _ { x \sim P _ { \text {data} } } [ \log D ( x ) ] + E _ { x \sim P _ { G } } [ \log ( 1 - D ( x ) ) ]
$$
在我们训练D网络的时候,我们要让V最大化,当我们训练G网络的时候我们要让V最小化,就是这么简单。因此哪怕数学推导那篇五六千字的博客不想看,实做也可以做。
实做上比较大的一个问题是我们实际上不能获取到全部真实图像样本和全部拟合图像样本。因此上面这道公式在实做上是搞不成的。
我们采取的方法是抽样。也就是从
$$
P _ { \text {data} }(x)
$$
中抽出m个样本,写作
$$
{ x ^ { 1 } , x ^ { 2 } , \ldots , x ^ { m } },
$$
再从
$$
P _ { \text {G} }(x)
$$
中抽出m个样本,写作
$$
{ \tilde { x } ^ { 1 } , \tilde { x } ^ { 2 } , \ldots , \tilde { x } ^ { m } },
$$
然后我们认为这m个样本的分布和总体的分布就差不多了。那么上面的公式就变成下面这个样子:
$$
\tilde { V } = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log D \left( x ^ { i } \right) + \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log \left( 1 - D \left( \tilde { x } ^ { i } \right) \right)
$$
当然可能有人会说,这样不就存在着误差吗?
是的,但这个误差会随着样本的增多和样本分布的合理化而减小,因此我们在选样本的时候还是要注意样本的数量和分布的合理性。不要搞10张样本就拿来训练,起码是“万”级别的,且如果你想生成的是猫的图像,不要选几万张“白”猫,因为那样生成网络和判别网络均会认为猫就是白色的,没有别的颜色。
OK,分析完误差之后我们假定样本是十分给力的,那么我们就能根据面这道公式来做计算。
首先看到D网络,我们要做的是最大化上面这个
$$
\tilde { V }
$$
,先来看看logx长什么样。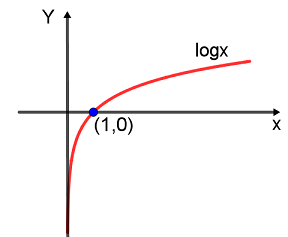
可以看出它是一个单调递增的函数,因此要
$$
\tilde { V }
$$
取得最大值,其实就是要
$$
\frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log D \left( x ^ { i } \right)和\frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log \left( 1 - D \left( \tilde { x } ^ { i } \right) \right)
$$
分别取得最大值。也就是要
$$
D \left( x ^ { i } \right)
$$
取得最大值,
$$
1 - D \left( \tilde { x } ^ { i } \right)
$$
取得最大值。因此,我们只需要在输入真实样本的时候尽量让D网络输出1,而输入拟合样本的时候让网络尽量输出0就搞定了。
这里有个非常神奇的地方,就是我们要求的这道式子跟二分类问题的交叉熵损失函数居然长的是一样的。我们先看看二分类问题的交叉熵损失函数长什么样:
$$
-\sum _ { i = 1 } ^ { m }p \left( x _ { i } \right)\log q \left( x _ { i } \right)-\sum _ { i = 1 } ^ { m }(1-p \left( x _ { i } \right))\log (1-q \left( \tilde { x } _ { i } \right))
$$
这里因为是二分问题,因此
$$
p \left( x _ { i } \right)
$$
在正样本中等于1,在负样本中等于0,这个时候上面的式子变成:
$$
-\sum _ { i = 1 } ^ { m }\log q \left( x _ { i } \right)-\sum _ { i = 1 } ^ { m }\log (1-q \left( \tilde { x } _ { i } \right))
$$
这道式子忽略掉常数项刚刚好是V取反。而我们本来求D网络就是求V取最大值的情况,一旦给V取反,则变成求最小值,直接等于损失函数的目标!真是不要太方便!
那么具体流程是什么呢?
1.从
$$
P _ { \text {data} }(x)
$$
中抽出m个样本,写作
$$
{ x ^ { 1 } , x ^ { 2 } , \ldots , x ^ { m } },
$$
再从
$$
P _ { \text {G} }(x)
$$
中抽出m个样本(也就是让G网络生成m个样本),写作
$$
{ \tilde { x } ^ { 1 } , \tilde { x } ^ { 2 } , \ldots , \tilde { x } ^ { m } }
$$
2.用二分问题的交叉熵损失函数作为损失函数,然后用样本对网络进行训练,完事,就是这么简单。
再来看看G网络,我们从前面已经知道G网络的目标是最小化:
$$
\tilde { V } = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log D \left( x ^ { i } \right) + \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log \left( 1 - D \left( \tilde { x } ^ { i } \right) \right)
$$
因为在训练G网络的时候,D网络是不变的,因此上面式子左边的一项是不变的,相当于一个常数。而对于最小化问题来说,常数是不影响结果的,因此我们其实是在最小化:
$$
\tilde { V }_G= \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log \left( 1 - D \left( \tilde { x } ^ { i } \right) \right)
$$
按理说按照上面所述已经可以开始写代码了。但实际上还有个操作上的问题,这个问题出在log(1−x)这个函数上,它长这样: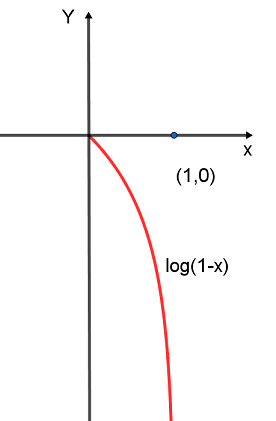
可以看到当x接近1的时候该函数相当的陡峭,而在0附近它却不是很陡(其实对log(1−x)求下导就可以知道它的导数的绝对值是逐步增大的,也就是它渐渐变陡)。这有什么问题呢?
问题就在于一开始的时候因为G网络的参数是接近随机的,基本上骗不过D网络,因此
$$
D \left( \tilde { x } ^ { i } \right)
$$
这个东西在一开始的时候总会输出接近0的数。而从上面我们知道,如果越接近0,那么log(1−x)这个损失函数就越平。而在训练后期,
$$
D \left( \tilde { x } ^ { i } \right)
$$
会慢慢增加(最理想是0.5),这个时候log(1−x)损失函数却越变越陡。这跟我们需要的是完全相反的!我们希望的是一开始训练快速收缩到最优解附近,然后慢慢调整找到最优解,而它反过来。因此虽然理论上那么列式是完全合理的,但实际上用这么一个损失函数会使得训练比较崩溃,十分的反直觉。因此为了解决这个问题,GAN用的损失函数并不是log(1−x),而是−log(x):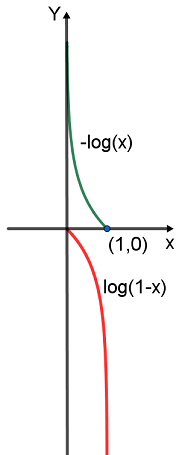
这个损失函数就牛逼了,单调性和log(1−x)一样,且陡峭程度变化完全符合我们的要求。因此我们真正训练G网络的时候用的是它。但这么改有个问题,就是我们本来G网络训练的是一个JS距离,现在训练的却不知道是个啥,只知道它大致等价于JS距离。不过这个问题好像也不是很要紧,总之我们训练的是这个式子:
$$
\tilde { V }_G= -\frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log \left(D \left( \tilde { x } ^ { i } \right) \right)
$$
看到这个式子再联系上面的D网络,聪明的你可能发现它长得和二分类问题的交叉熵损失函数输入正样本的情况又是一模一样的(除了个没多大所谓的常数项)。这在我们实际操作中简直不要太方便!具体流程是:
1.从z中抽出m个样本,写作
$$
{ \tilde { z } ^ { 1 } , \tilde { z } ^ { 2 } , \ldots , \tilde { z } ^ { m } }
$$
2.用二分问题的交叉熵损失函数作为损失函数,然后用样本对网络进行训练,大功告成!
那么具体的训练过程大概总结下是这个样子的,先定住G网络训练几次D网络,再定住D网络训练一次G网络,循环往复就行了。为什么是几次和一次呢?
首先,因为我们希望D网络这把尺子准一点,最好每次都找到全局最优解,这样能更好的指导G网络。
其次,我们希望G网络每次不要更新太多,具体可见下图: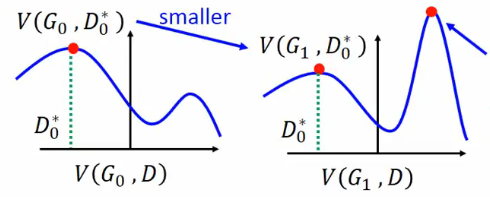
如果更新太多,G网络的形状可能会从左边变到右边,这样D网络的最大值点会到处飘,比较难训练。
下面放上实现代码,非常简单。主要参考的《深度学习框架PyTorch:入门与实践》这本书的代码,本人把其他复杂的东西删掉了,就剩下最简单的实现部分,这样看起来清楚点。
1 | # coding:utf-8 |
1 | # coding:utf-8 |
一开始训练得到的图如下的一坨:
后面训练了一百多个轮次之后渐渐好了起来:

可以看到有些图片已经有模有样了,但有些还蛮崩坏的。这跟原生GAN的一些缺陷有关系,比如说DD网络容易过拟合,或者GG网络分布远远不足以覆盖目标子集,距离一直很大等等。这个在后面的改进版本逐步得到解决,会在以后研究到的时候跟大家分享。当然也可以直接去Bilibili看看李宏毅教授的视频,讲得非常给力!
另外如果希望用可视化工具visdom,可以将main.py的代码修改如下:
1 | # coding:utf-8 |