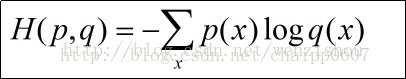JS散度
前面我们介绍了相对熵(KL散度)的概念,知道了它可以用来表示两个概率分布之间的差异,但有个不大好的地方是它并不是对称的,因此有时用它来训练神经网络会有顺序不同造成不一样的训练结果的情况(其实个人觉得也就是训练时间差异罢了,也没那么严重)。为了克服这个问题,有人就提出了一个新的衡量公式,叫做JS散度,式子如下:
$$
J S \left( P _ { 1 } | P _ { 2 } \right) = \frac { 1 } { 2 } K L \left( P _ { 1 } | \frac { P _ { 1 } + P _ { 2 } } { 2 } \right) + \frac { 1 } { 2 } K L \left( P _ { 2 } | \frac { P _ { 1 } + P _ { 2 } } { 2 } \right)JS(P1∥P2)=21KL(P1∥2P1+P2)+21KL(P2∥2P1+P2)
$$
如果有一点数学功底的人可以轻易看出这个公式对于
$$
P _ { 1 }和P _ { 2 }
$$
是对称的,而且因为是两个KL的叠加,由相对熵的文章我们知道KL的值一定是大于等于0的,因此这个公式也一定大于等于0。
现在只剩下一个关键问题,就是什么时候等于0的问题了。同样参考相对熵的文章我们知道当两个分布相同的时候等于0,那么换到这里,也就是:
$$
P _ { 1 }=\frac { P _ { 1 } + P _ { 2 } }{ 2 }\ \qquad 且 \qquad P _ { 2 }=\frac { P _ { 1 } + P _ { 2 } } { 2 }P_ { 1 }=2P_ { 1 }+P_ { 2 } 且P_ { 2 }=2P_ { 1 }+P_ { 2 }
$$
的时候。可以轻易看出来,JS散度等于0的时候跟KL散度一样,就是
$$
P _ { 1 }和P _ { 2 }
$$
完全一样的时候。那么推到这里,用JS散度来表达两个概率分布的差异就问题不大了。
其实本人在看相对熵和JS散度的时候一直有疑问,就是当两个概率分布不一样的时候,它们的值是不是会随着距离的变大而变大,也就是说这两个公式跟概率分布的距离到底是不是一个单调的关系,但我没有看到别人在说这件事情。我自己想了半天之后得出的结论是不一定,可能随着概率分布的表达式不一样而有所变化。
当然因为没有人讲这件事我至今也不知道这样想是不是对的,因此有老哥想明白了麻烦留个言告诉我。