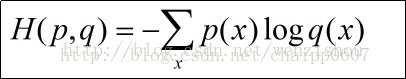君子兰萧宇的博客

概述通过本文我们来一起看一些用于人工智能的高质量AI库，它们的优点和缺点，以及它们的一些特点。 人工智能（AI）已经存在很长时间了。然而，由于这一领域的巨大进步，近年来它已成为一个流行语。人工智能曾经被称为一个完整的书呆子和天才的领域，但由于各种开发库和框架的发展，它已经成为一个友好的IT领域，并有很多人正走进它。 在这篇文章中，我们将研究用于人工智能的优质库，它们的优缺点以及它们的一些特征。让我们深入并探索这些人工智能库的世界！ 1. TensorFlow“使用数据流图表的可伸缩机器学习的计算” 语言：C ++或Python。 当进入AI时，你会听到的第一个框架之一就是Google的TensorFlow。 TensorFlow是一个使用数据流图表进行数值计算的开源软件。这个框架被称为具有允许在任何CPU或GPU上进行计算的架构，无论是台式机、服务器还是移动设备。这个框架在Python编程语言中是可用的。 TensorFlow对称为节点的数据层进行排序，并根据所获得的任何信息做出决定。 优点： 使用易于学习的语言（Python）。 使用计算图表抽象。 用于TensorBoard的可 ...

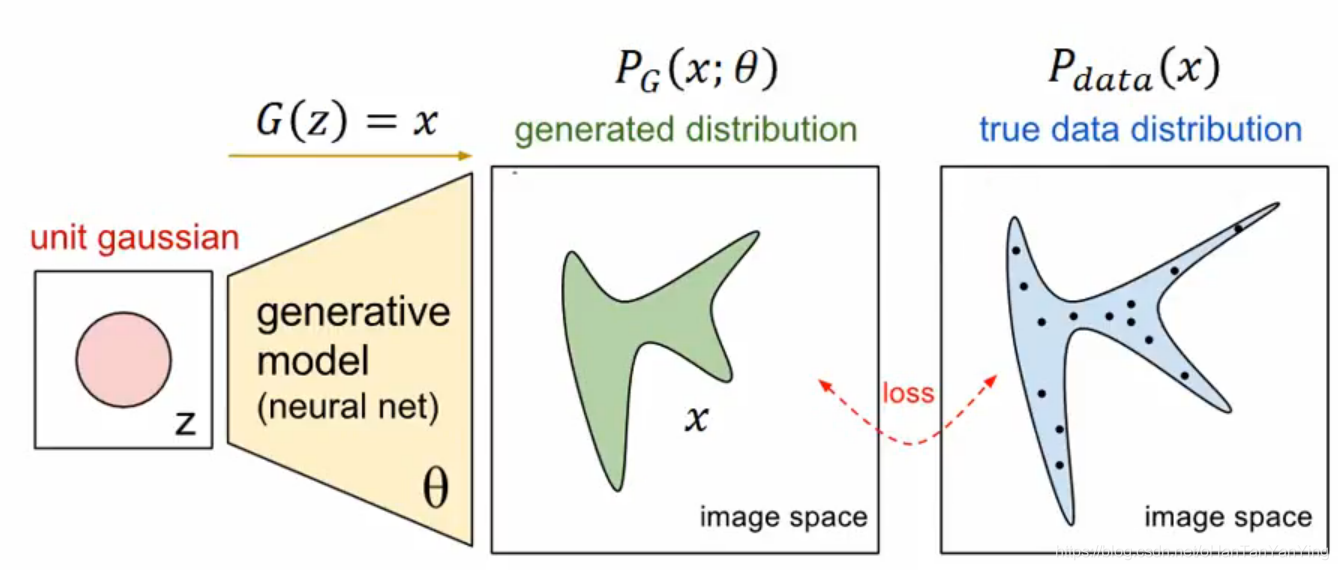
由上面一篇文章我们已经知道了，如果我们从真实数据分布里面取n个样本，根据给定样本我们可以列出其出现概率的表达式，那么生成这N个样本数据的似然(likelihood)就是$$l ( \theta )= \prod _ { i = 1 } ^ { N } p \left( x _ { i } | \theta \right)$$我们要找到\thetaθ来最大化这个函数，便是极大似然估计，公式如下：$$\hat { \theta } = \arg \max _ { \theta } H ( \theta ) = \arg \max _ { \theta } \ln l ( \theta ) = \arg \max _ { \theta } \sum _ { i = 1 } ^ { N } \ln p \left( x _ { i } | \theta \right)$$那么下面我们来看看GAN的推导。 在极大似然估计中，我们假定要求的事物有一个固定的模型，写作$$P_{data}(x)Pdata(x)$$，但这个模型十分复杂，我们无法完全彻底的去刻画它，只能列一个带有参数的式子，然后用模型抽 ...

上一篇文章我们强力推导了GAN的数学公式，它就是：$$V = E _ { x \sim P _ { \text {data} } } [ \log D ( x ) ] + E _ { x \sim P _ { G } } [ \log ( 1 - D ( x ) ) ]$$在我们训练D网络的时候，我们要让V最大化，当我们训练G网络的时候我们要让V最小化，就是这么简单。因此哪怕数学推导那篇五六千字的博客不想看，实做也可以做。 实做上比较大的一个问题是我们实际上不能获取到全部真实图像样本和全部拟合图像样本。因此上面这道公式在实做上是搞不成的。 我们采取的方法是抽样。也就是从$$P _ { \text {data} }(x)$$中抽出m个样本，写作$${ x ^ { 1 } , x ^ { 2 } , \ldots , x ^ { m } }，$$再从$$P _ { \text {G} }(x)$$中抽出m个样本，写作$${ \tilde { x } ^ { 1 } , \tilde { x } ^ { 2 } , \ldots , \tilde { x } ^ { m } }，$$然后我们 ...

前面我们介绍了相对熵（KL散度）的概念，知道了它可以用来表示两个概率分布之间的差异，但有个不大好的地方是它并不是对称的，因此有时用它来训练神经网络会有顺序不同造成不一样的训练结果的情况（其实个人觉得也就是训练时间差异罢了，也没那么严重）。为了克服这个问题，有人就提出了一个新的衡量公式，叫做JS散度，式子如下：$$J S \left( P _ { 1 } | P _ { 2 } \right) = \frac { 1 } { 2 } K L \left( P _ { 1 } | \frac { P _ { 1 } + P _ { 2 } } { 2 } \right) + \frac { 1 } { 2 } K L \left( P _ { 2 } | \frac { P _ { 1 } + P _ { 2 } } { 2 } \right)JS(P1∥P2)=21KL(P1∥2P1+P2)+21KL(P2∥2P1+P2)$$如果有一点数学功底的人可以轻易看出这个公式对于$$P _ { 1 }和P _ { 2 }$$是对称的，而且因为是两个KL的叠加，由相对熵的文章我们知道KL的值一定是 ...

在很多二分类问题中，特别是正负样本不均衡的分类问题中，常使用交叉熵作为loss对模型的参数求梯度进行更新，那为何交叉熵能作为损失函数呢，我也是带着这个问题去找解析的。 以下仅为个人理解，如有不当地方，请读到的看客能指出。 我们都知道，各种机器学习模型都是模拟输入的分布，使得模型输出的分布尽量与训练数据一致，最直观的就是MSE（均方误差，Mean squared deviation), 直接就是输出与输入的差值平方，尽量保证输入与输出相同。这种loss我们都能理解。 以下按照（1）熵的定义（2）交叉熵的定义 (3) 交叉熵的由来 （4）交叉熵作为loss的优势 作为主线来一步步理清思路。 （1）熵的定义 各种熵的名称均来自信息论领域，这方面的背景就不介绍了，随便就能找到很多。 根据维基的定义，熵的定义如下：熵是接收的每条消息中包含的信息的平均量，又被称为信息熵、信源熵、平均自信息量。直白地解释就是信息中含的信息量的大小，其定义如下： 其曲线如下所示： 可以看出，一个事件的发生的概率离0.5越近，其熵就越大，概率为0或1就是确定性事件，不能为我们带信息量。也可以看作是一件事我们越难猜测 ...

我们简单介绍了相对熵的概念，知道了相对熵可以用来表达真实事件和理论拟合出来的事件之间的差异。 相对熵的公式如下：$$D _ { K L } ( p | q ) = \sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log p \left( x _ { i } \right)-\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)$$可以看到前面一项是真实事件的信息熵取反，我们可以直接写成$$D _ { K L } ( p | q ) = -H(p)-\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)$$在神经网络训练中，我们要训练的是$$q ( x _ { i })$$使得其与真实事件的分布越接近越好，也就是说在神经网络的训练中，相对熵会变的部分只有后面的部分，我们希望它越小越好，而前面的那部分是不变的。因此我们可以把 ...

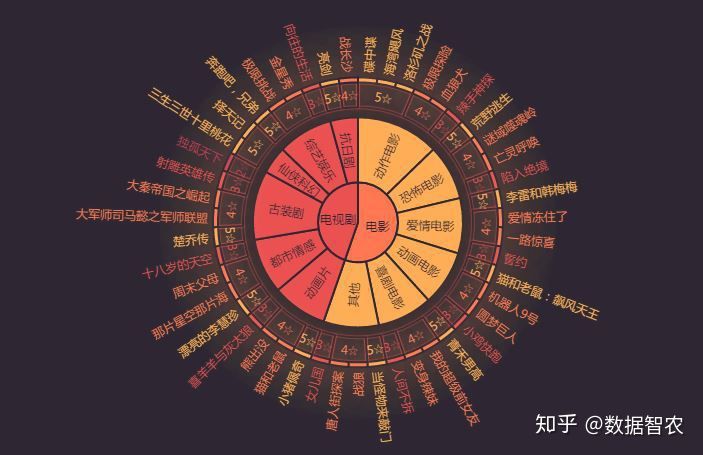
获奖经历： 2017年4月:美国大学生数学建模竞赛二等奖 2017年11月:数学建模竞赛国家一等奖 2017年11月:数学竞赛国家二等奖 2018年4月:美国大学生数学建模竞赛二等奖 2018年5月:泰迪杯数据挖掘竞赛国家二等家 兴趣爱好：羽毛球，读书 个人生活照：（1-2张） 一、实验目的 1、实验背景 本实验项目来自于第六届泰迪杯数据挖掘竞赛，共包含用户观看信息和电视产品信息两组数据，通过对数据进行处理，实现产品的精准营销推荐，并将并将结果进行可视化展示。 2、实验目的 基于电视产品及用户信息数据对产品进行精准营销推荐，并将结果进行可视化展示。主要实现以下两个目的： （1）产品的精准营销推荐 根据用户观看记录信息数据，分析用户的收视偏好，并给出电视产品的营销推荐方案。 （2）相似偏好用户的产品打包推荐 为了更好地为用户服务，扩大营销范围，利用数据对相似偏好的用户进行分类（用户标签），对产品进行分类打包（产品标签），并给出营销推荐方案。 3、实验内容与要求 （1）对数据进行处理，并根据用户的收视信息对用户偏好进行分析，将分析结果用图像进行表示。 （2）整理产品信息，重新对产品分类， ...

似然（likelihood）这个词其实和概率（probability）是差不多的意思，但是在统计里面，似然函数和概率函数却是两个不同的概念。 对于函数：P(x∣θ)，输入有两个：x表示某一个具体的数据；θ表示模型的参数。 如果θ是确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。 比如我们已经知道了一个箱子里有19个黑球和一个白球，现在问你从箱子里抽出两个球，是两个黑球的概率是多少，这个时候我们的模型参数是完全知道了，就是19个黑球和一个白球，不知道的是抽出的具体的球是什么。这个时候，P(x∣θ)就是概率函数。 如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function)，它描述对于不同的模型参数，出现x这个样本点的概率是多少。 比如我们有一箱子球，已经从里面抽出了1个黑球8个白球，问你箱子里面黑球和白球的分布模型参数是什么。这个时候我们是不知道箱子里面的具体情况的，但我们知道抽出球的样本分布，那么我们要用样本的分布来评估箱子里的球的模型分布，这个时候P(x∣θ)就是似然函数。 ...

我们简单介绍了香农信息量的概念，由香农信息量我们可以知道对于一个已知概率的事件，我们需要多少的数据量能完整地把它表达清楚，不与外界产生歧义。但对于整个系统而言，其实我们更加关心的是表达系统整体所需要的信息量。比如我们上面举例的aaBaaaVaaaaa这段字母，虽然B和V的香农信息量比较大，但他们出现的次数明显要比a少很多，因此我们需要有一个方法来评估整体系统的信息量。 相信你可以很容易想到利用期望这个东西，因此评估的方法可以是：“事件香农信息量×事件概率”的累加。这也正是信息熵的概念。 如aaBaaaVaaaaa这段字母，信息熵为：$$-\frac{5}{6}log_2\frac{5}{6}-2×\frac{1}{12}log_2\frac{1}{12}=0.817$$abBcdeVfhgim这段字母，信息熵为：$$-12×\frac{1}{12}log_2\frac{1}{12}=3.585$$从数值上可以很直观地看出，第二段字母信息量大，和观察相一致。 对于连续型随机变量，信息熵公式变为积分的形式，如下： $$H ( p ) = H ( X ) = \mathrm { E } _ ...

共轭函数在最近火的不行的Gan生成对抗神经网络进阶版本的数学推理中有着神奇的作用，因此在这边记录下。 共轭函数的定义为：$$f ^ { * } ( t ) = \max _ { x \in \operatorname { dom } ( f ) } { x t - f ( x ) }$$当然如果去百度它不是这么写的，但这么写和一般的写法等价。 这个公式的$$x \in \operatorname { dom } ( f )$$表示x要在f的定义域内取值，这个蛮好理解的，不在定义域内就算不了。 那它具体在干一件什么事情呢？ 可以看到式子的自变量是t，而当t定住后，式子希望在定义域内找到一个x使得右边大括号内的式子取得最大值。 它的物理意义是什么呢？ 可以看到当t定住的时候，式子其实变成了y=xt−f(x)，如果高兴也可以再把左右拆开，这样就会发现左边其实是以t为斜率的一根直线，而右边则是x的函数，那么max这货就是要找到原函数f(x)和以t为斜率的直线的最大距离点对应的$$x ^ { * }。$$ 说实在的，上面的解释我一看就懂，但完全不知所谓，心中十万只草泥马。最核心的问题在于，这个物 ...