人工智能神经网络四种算法
人工神经网络的许多算法已在智能信息处理系统中获得广泛采用,尤为突出是是以下4种算法:ART网络、LVQ网络、Kohonen网络Hopfield网络,下面就具体介绍一下这这四种算法:
1.自适应谐振理论(ART)网络
自适应谐振理论(ART)网络具有不同的方案。一个ART-1网络含有两层一个输入层和一个输出层。这两层完全互连,该连接沿着正向(自底向上)和反馈(自顶向下)两个方向进行。
当ART-1网络在工作时,其训练是连续进行的,且包括下列算法步骤:
(1)对于所有输出神经元,如果一个输出神经元的全部警戒权值均置为1,则称为独立神经元,因为它不被指定表示任何模式类型。
(2)给出一个新的输入模式x。
(3)使所有的输出神经元能够参加激发竞争。
(4)从竞争神经元中找到获胜的输出神经元,即这个神经元的x·W值为最大;在开始训练时或不存在更好的输出神经元时,优胜神经元可能是个独立神经元。
(5)检查该输入模式x是否与获胜神经元的警戒矢量V足够相似。
(6)如果r≥p,即存在谐振,则转向步骤(7);否则,使获胜神经元暂时无力进一步竞争,并转向步骤(4),重复这一过程直至不存在更多的有能力的神经元为止。
2.学习矢量量化(LVQ)网络
学习矢量量化(LVQ)网络,它由三层神经元组成,即输入转换层、隐含层和输出层。该网络在输入层与隐含层之间为完全连接,而在隐含层与输出层之间为部分连接,每个输出神经元与隐含神经元的不同组相连接。
最简单的LVQ训练步骤如下:
(1)预置参考矢量初始权值。
(2)供给网络一个训练输入模式。
(3)计算输人模式与每个参考矢量间的Euclidean距离。
(4)更新最接近输入模式的参考矢量(即获胜隐含神经元的参考矢量)的权值。如果获胜隐含神经元以输入模式一样的类属于连接至输出神经元的缓冲器,那么参考矢量应更接近输入模式。否则,参考矢量就离开输人模式。
(5)转至步骤(2),以某个新的训练输入模式重复本过程,直至全部训练模式被正确地分类或者满足某个终止准则为止。
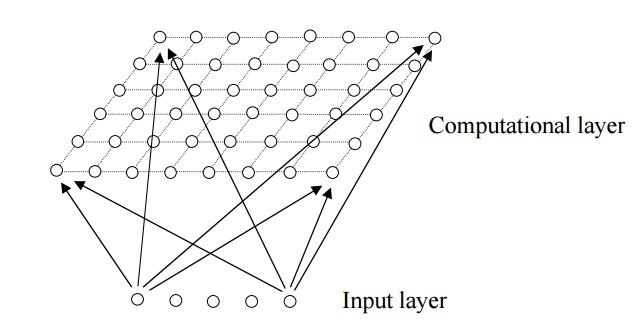
3.Kohonen网络
Kohonen网络或自组织特征映射网络含有两层,一个输入缓冲层用于接收输入模式,另一个为输出层,输出层的神经元一般按正则二维阵列排列,每个输出神经元连接至所有输入神经元。连接权值形成与已知输出神经元相连的参考矢量的分量。
训练一个Kohonen网络包含下列步骤:
(1)对所有输出神经元的参考矢量预置小的随机初值。
(2)供给网络一个训练输入模式。
(3)确定获胜的输出神经元,即参考矢量最接近输入模式的神经元。参考矢量与输入矢量间的Euclidean距离通常被用作距离测量。
(4)更新获胜神经元的参考矢量及其近邻参考矢量。这些参考矢量(被引至)更接近输入矢量。对于获胜参考矢量,其调整是最大的,而对于离得更远的神经元,减少调整个神经元邻域的大小随着训练的进行而相对减小,到训练结束,只有获胜神经元的参考矢量被调整。
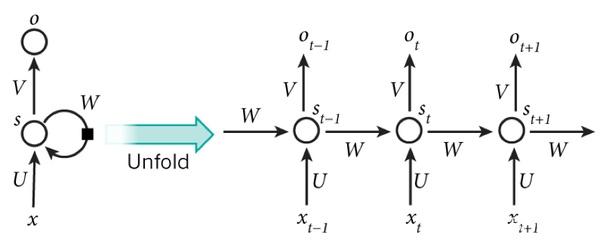
4.Hopfield网络
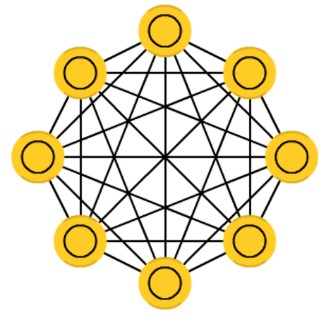
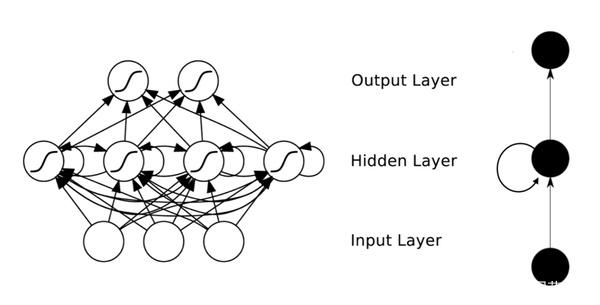
Hopfield网络是一种典型的递归网络,这种网络通常只接受二进制输入(0或1)以及双极输入(+1或-1)。它含有一个单层神经元,每个神经元与所有其他神经元连接,形成递归结构。
上图为Hopfield神经网络结构图。
首先,网络结构上,Hopfield神经网络是一种单层互相全连接的反馈型神经网络。每个神经元既是输入也是输出,网络中的每一个神经元都将自己的输出通过连接权传送给所有其它神经元,同时又都接收所有其它神经元传递过来的信息。即:网络中的神经元在t时刻的输出状态实际上间接地与自己t-1时刻的输出状态有关。神经元之间互连接,所以得到的权重矩阵将是对称矩阵。
同时,Hopfield神经网络成功引入能量函数的概念,使网络运行地稳定性判断有了可靠依据。基本的Hopfield神经网络是一个由非线性元件构成的全连接型单层递归系统。其状态变化可以用差分方程来表示。递归型网络的一个重要特点就是它具有稳定状态‘当网络达到稳定状态的时候,也就是它的能量函数达到最小的时候。这里的能量函数不是物理意义上的能量函数,而是在表达形式上与物理意义上的能量概念一致,即它表征网络状态的变化趋势,并可以依据Hopfield网络模型的工作运行规则不断地进行状态变化,最终能够到达具有某个极小值的目标函数。网络收敛就是指能量函数达到极小值。
如果把一个最优化在着递归信号,网络的状态是随时间的变化而变化的,其运动轨迹必然存在着稳定性的问题。这就是递归网络与前向网络在网络性能分析上最大的区别之一在使用递归网络时,必须对其稳定性进行专门的分析与讨论,合理选择网络的参数变化范围,才能确保递归网络的正常工作。
Hopfield神经网络模型有离散型和连续性两种,离散型适用于联想记忆,连续性适合处理优化问题。