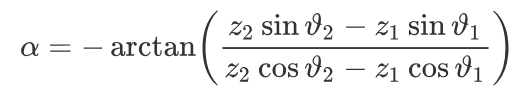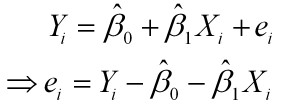卷积与转置卷积
卷积与转置卷积
得益于神经网络崛起,卷积成为近些年大热的数学词汇,不再只是待在信号处理这门要命的课程之中。
关于卷积在图像处理中的应用,操作部分看上图就明白了:假设输入图像的大小为 5 x 5,局部感受野(或称卷积核)的大小为 3 x 3,那么输出层一个神经元所对应的计算过程如上图所示。动态一点的话也可以看下面的动图。而为什么要这么算,如果学过一点图像处理就很好说明,图像处理的经典边缘提取算法如canny,sobel等,或者其他一些经典算法,其实归根结底就是一个卷积过程,只不过里面的卷积核是人为设定的而已。相比于神经网络的全连接层,用卷积层更加能够快速提取到图像的局部信息,也因此更有旋转不变性等的优势,此外需要训练的参数量相比全连接也要少的多。
在实做方面,为了效率,往往会把卷积计算用矩阵来做。
假设一个卷积操作,它的输入是 4x4,卷积核大小是 3x3,步长为 1x1,输出则为 2x2,如下所示:
我们将其从左往右,从上往下以的方式展开,
输入矩阵可以展开成维数为 [16, 1] 的矩阵,记作 x
输出矩阵可以展开成维数为 [4, 1] 的矩阵,记作 y
卷积核可以表示为 [4, ...
拷贝网页上的公式到本地
有时在写文章或者搞别的东西的时候需要用到别人的公式,然而一般这些公式都是复制不了的,如果这个时候一个个去打可以说相当要命。然而我们可以通过:mathpix这个神器轻轻松松解决这个问题。有了它之后,在哪看到公式直接截图就可以帮我们翻译成latex公式。就像上面这个,一截就变成了下面的这一串latex公式描述1\alpha = - \arctan \left( \frac { z _ { 2 } \sin \vartheta _ { 2 } - z _ { 1 } \sin \vartheta _ { 1 } } { z _ { 2 } \cos \vartheta _ { 2 } - z _ { 1 } \cos \vartheta _ { 1 } } \right)
接着,我们可以把这段描述放到Typora等markdown工具中,公式又将美好的出现在我们面前。当然到这里其实是不 ...
机器学习经典算法之-----最小二乘法
最小二乘法
我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢? 监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归分析中,如果只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。对于二维空间线性是一条直线;对于三维空间线性是一个平面,对于多维空间线性是一个超平面…
对于一元线性回归模型, 假设从总体中获取了n组观察值(X1,Y1),(X2,Y2), …,(Xn,Yn)。对于平面中的这n个点,可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看,这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为:使总的拟合误差(即总残差)达到最小。有以下三个标准可以选择:
(1)用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。 (2)用“残差绝对值和最小”确定直线位置也是 ...
极大似然估计(MLE)
我们已经了解了似然函数是什么,但怎么去把里面的θ给求出来是个更加关键的问题。这篇我们将来探讨下这个问题。
还是先举一个例子,假设有一个造币厂生产某种硬币,现在我们拿到了一枚这种硬币,想试试这硬币是不是均匀的。即想知道抛这枚硬币,正反面出现的概率(记为θ)各是多少?
这是一个统计问题,回想一下,解决统计问题需要什么? 数据!
于是我们拿这枚硬币抛了10次,得到的数据x_0x0是:反正正正正反正正正反。我们想求的正面概率θ是模型参数,而抛硬币模型是二项分布(除非硬币立起来,那么这个时候要马上去买彩票,还搞什么算法)。
那么,出现实验结果x0(即反正正正正反正正正反)的似然函数是多少呢?我们是这样列式的:$$f \left( x _ { 0 } , \theta \right) = ( 1 - \theta ) \times \theta \times \theta \times \theta \times \theta \times ( 1 - \theta ) \times \theta \times \theta \times \theta \times ( 1 - \theta ) ...
深度学习2---任意结点数的三层全连接神经网络
上一篇文章:深度学习1—最简单的全连接神经网络 我们完成了一个三层(输入+隐含+输出)且每层都具有两个节点的全连接神经网络的原理分析和代码编写。本篇文章将进一步探讨如何把每层固定的两个节点变成任意个节点,以方便我们下一篇文章用本篇文章完成的网络来训练手写字符集“mnist”。 对于前向传播,基本上没有什么变化,就不用说了。主要看看后向传播的梯度下降公式。先放上上篇文章的网络图。 上篇文章我们推知,含有两个节点的隐含层到输出层的权值对误差的偏导数,公式如下: $$ \frac{\partial E_{总}}{\partial W_{11}^{(2)}}=(O_{1}-T_{1})*O_{1}(1-O_{1})*Y_{1}$$ 而含有两个节点的输入层到隐含层的权值对于误差梯度的偏导数公式如下: $$\frac{\partial E_{总}}{\partial W_{11}^{(1)}}=((O_{1}-T_{1})*O_{1}(1-O_{1})*W_{11}^{(2)}+(O_{2}-T_{2})*O_{2}(1-O_{2})*W_{21}^{(2)})*Y_{1}(1-Y_{ ...
深度学习1---最简单的全连接神经网络
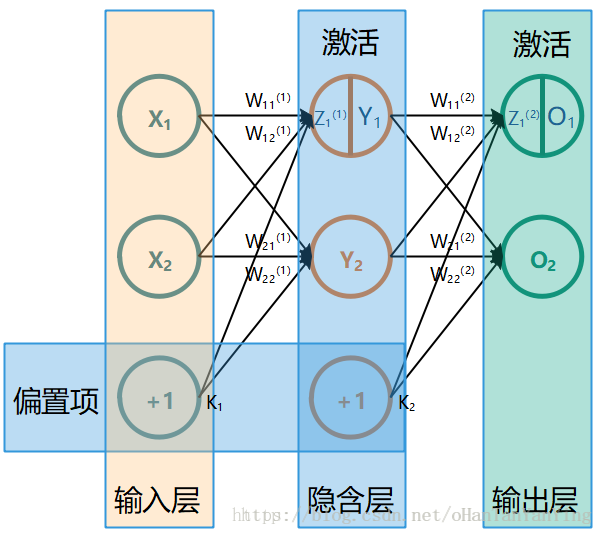
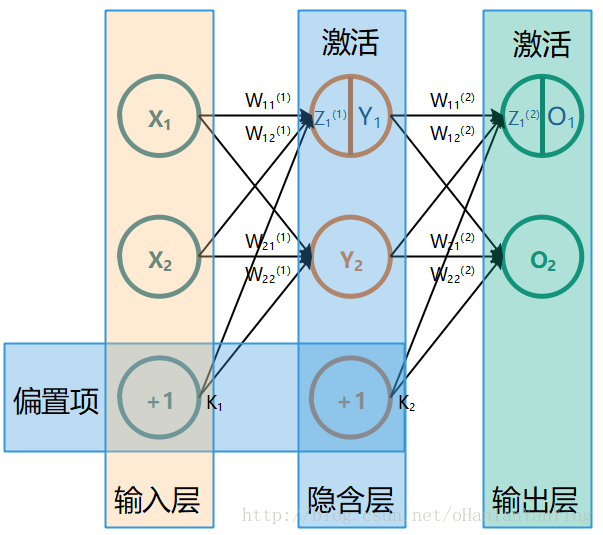
本文有一部分内容参考以下两篇文章: 一文弄懂神经网络中的反向传播法——BackPropagation 神经网络 最简单的全连接神经网络如下图所示(这张图极其重要,本文所有的推导都参照的这张图,如果有兴趣看推导,建议保存下来跟推导一起看):
它的前向传播计算过程非常简单,这里先讲一下:
前向传播
$$\begin{aligned}Y_{1} &=f\left(W_{11}^{(1)} X_{1}+W_{12}^{(1)} X_{2}+K_{1}\right) \Y_{2} &=f\left(W_{21}^{(1)} X_{1}+W_{22}^{(1)} X_{2}+K_{1}\right) \O_{1} &=f\left(W_{11}^{(2)} Y_{1}+W_{12}^{(2)} Y_{2}+K_{2}\right) \O_{2} &=f\left(W_{21}^{(2)} Y_{1}+W_{22}^{(2)} Y_{2}+K_{2}\right)\end{aligned}$$ 具体的,如果代入实际数值,取$$\begin{array ...
海淘新手入门必看——2018最新美国亚马逊海淘攻略!含海淘转运攻略海淘教程
海淘是什么相信大家应该都了解,在蒸蒸日上的海淘大军里,很多人在海淘购物之前担心很多问题,因此在海淘大门前徘徊许久。在没开始海淘钱我一是其中的一分子 。下面和朋友们说说亚马逊的攻略希望可以帮助那些徘徊在海淘门前的你们。
详细介绍一下在美国亚马逊购物的攻略!先给大家说一下,海淘一点都不复杂,这个教程虽然写了很长,但其实真正操作起来就几个步骤,大家不要看到这么长的教程就犹豫了!最关键的是第一次需要注册,填各种信息,所以第一次有点麻烦,有了第一次,以后海淘,就剩下爽了!(一)首先你需要准备一张信用卡,美国亚马逊支持双币信用卡、单币银联卡,都无手续费,直接以实时汇率转换成人民币结算! (帮主现在用的最多的是浦发信用卡,海淘最高有25%的返现,平时看电影、吃饭也经常会有浦发信用卡的折扣,网上申请也非常方便 ) (二)其次对于英语不太好的亲来说,一个翻译软件是很有必要的,不过现在都有网页版的在线翻译,把要翻译的句子粘贴过去,基本解决问题。然后是换算。美国的重量采取的是磅,一磅等于454克,这样心里就有个谱了,因为运费牵扯到重量的。(三)由于大部分美国网站都不能直运回中国(美国亚马逊部分商品可直邮,直 ...
深度学习3—用三层全连接神经网络训练MNIST手写数字字符集
上一篇文章:深度学习2—任意结点数的三层全连接神经网络 距离上篇文章过去了快四个月了,真是时光飞逝,之前因为要考试所以耽误了更新,谁知道考完试之前落下的接近半个学期的工作是如此之多,以至于弄到现在才算基本填完坑,实在是疲惫至极。 另外在这段期间,发现了一本非常好的神经网络入门书籍,本篇的很多细节问题本人就是在这本书上找到的答案,强烈推荐一下:
上篇文章介绍了如何实现一个任意结点数的三层全连接神经网络。本篇,我们将利用已经写好的代码,搭建一个输入层、隐含层、输出层分别为784、100、10的三层全连接神经网络来训练闻名已久的mnist手写数字字符集,然后自己手写一个数字来看看网络是否能比较给力的工作。 在正式做之前,还是按照惯例讲几个会用到的知识点。
mnist数字字符集的结构解析,这个我单独写了一篇文章来做介绍了,如有需要了解请先移步:深度学习3番外篇—mnist数据集格式及转换
我们之前都是直接放入几个数作为输入,然后给网络几个数作为目标来训练网络的,而mnist手写字符集给我们的是一堆手写的2828像素的图片还有图片对应的手写数字标签,我们怎么对它进行转换? ...
琴生(jensen)不等式
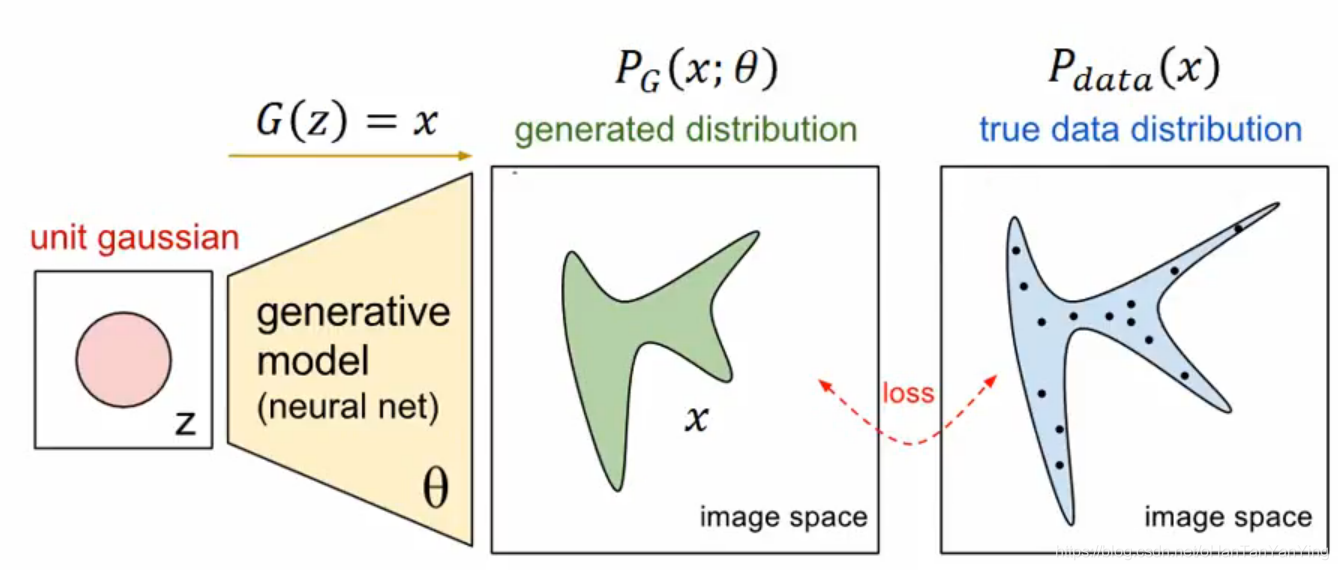
在Gan生成对抗神经网络中会用到Jensen不等式,因此做下记录。
Jensen不等式告诉我们:如果f是在区间[a,b]上的凸函数(就是导数一直增长的函数,或者说是导数的导数大于0的函数),x是随机变量,那么有:$$E(f(x))≥f(E(x))$$也就是说函数f ff的期望大于等于期望的函数。
下面来看看怎么证明,我们假设$$x_{1}, x_{2}, \ldots \ldots x_{n}$$都是区间[a,b]内的数,且$$x_{1} \leq x_{2} \leq, \ldots \ldots x_{n}$$,则上式可以写成下面这个形式:$$a_{1} f\left(x_{1}\right)+a_{2} f\left(x_{2}\right)+\ldots \ldots+a_{n} f\left(x_{n}\right) \geq f\left(a_{1} x_{1}+a_{2} x_{2}+\ldots \ldots+a_{n} x_{n}\right)$$其中$$\sum_{i=1}^{n} a_{i}=1 \text { 且 } a_{i}>0$$当n = 1时,式子 ...
相对熵(KL散度)
我们简单介绍了信息熵的概念,知道了信息熵可以表达数据的信息量大小,是信息处理一个非常重要的概念。
对于离散型随机变量,信息熵公式如下:$$H ( p ) = H ( X ) = \mathrm { E } _ { x \sim p ( x ) } [ - \log p ( x ) ] = -\sum_{i=1}^n p ( x )\log p ( x )$$对于连续型随机变量,信息熵公式如下:$$H ( p ) = H ( X ) = \mathrm { E } _ { x \sim p ( x ) } [ - \log p ( x ) ] = - \int p ( x ) \log p ( x ) d x$$注意,我们前面在说明的时候log是以2为底的,但是一般情况下在神经网络中,默认以e为底,这样算出来的香农信息量虽然不是最小的可用于完整表示事件的比特数,但对于信息熵的含义来说是区别不大的。其实只要这个底数是大于1的,都能用来表达信息熵的大小。
本篇我们来看看机器学习中比较重要的一个概念—相对熵。相对熵,又被称为KL散度或信息散度,是两个概率分布间差异的非对称性度量 。在信息论中 ...