上一篇文章:深度学习2—任意结点数的三层全连接神经网络
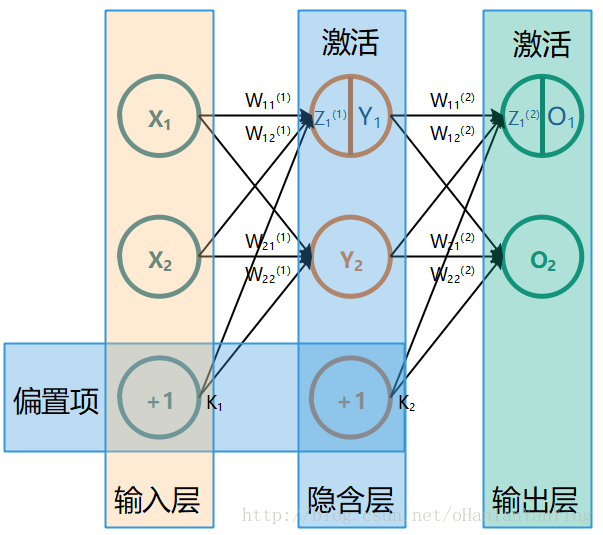
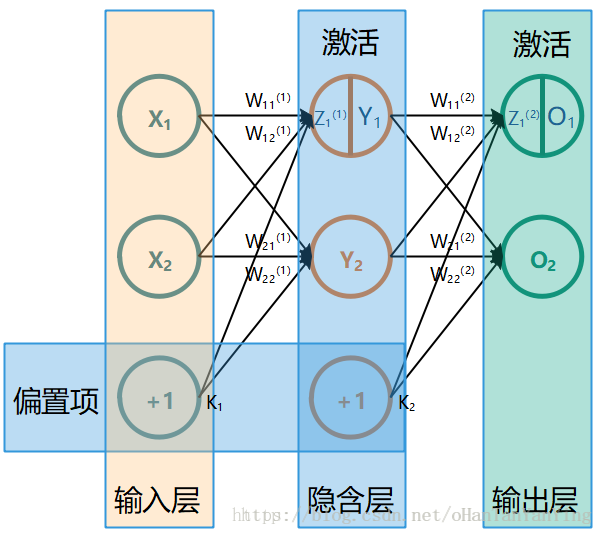
上篇文章介绍了如何实现一个任意结点数的三层全连接神经网络。本篇,我们将利用已经写好的代码,搭建一个输入层、隐含层、输出层分别为784、100、10的三层全连接神经网络来训练闻名已久的mnist手写数字字符集,然后自己手写一个数字来看看网络是否能比较给力的工作。
mnist数字字符集的结构解析,这个我单独写了一篇文章来做介绍了,如有需要了解请先移步:深度学习3番外篇—mnist数据集格式及转换
我们之前都是直接放入几个数作为输入,然后给网络几个数作为目标来训练网络的,而mnist手写字符集给我们的是一堆手写的2828像素的图片还有图片对应的手写数字标签,我们怎么对它进行转换? 28=784个像素直接作为输入,然后用0~9总共十个数作为输出目标的指引(当标签是“5”,则目标输出为0.01、0.01、0.01、0.01、0.01、0.99、0.01、0.01、0.01、0.01,依次类推)。
我们前面只确定了输入和输出层的节点个数,隐含层的节点个数还不知道,那我们怎么选取呢?答案可能让人难过,没有绝对正确的公式,只有几个经验公式(似乎有优化算法可以确定隐含层节点个数,后面如有需要开一篇专门讨论):
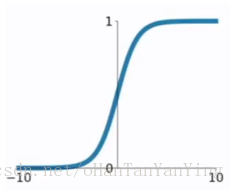
因为这次的输入节点有784个,算是比较多的,要十分注意在初始化网络参数的时候要避免参数与输入节点的积之和过大的情况出现。因为我们用的是sigmod函数作为激活函数,它的波形如下图所示:
最后,我们要判断输出的是否准确,则先做前向传播,得到10个输出之后,找到最大的一个跟标签对比,如果相同则网络预测正确。
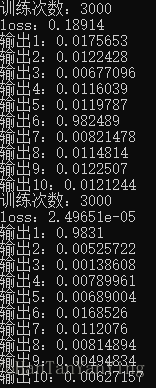
那么,原理介绍完了,我们先对下图所示的第一、二张图像和相应的标签进行训练,主要代码如下(整个工程的代码会在最后面给出):
1 2 3 4 5 6 7 8 9 10 11 for (size_t count = 0; count < 3000; count++) { mnet.forwardPropagation(mNumImg[0].inputdata);//前向传播 mnet.backPropagation(mNumImg[0].outputdata);//反向传播 mnet.forwardPropagation(mNumImg[1].inputdata);//前向传播 mnet.backPropagation(mNumImg[1].outputdata);//反向传播 } mnet.forwardPropagation(mNumImg[0].inputdata); mnet.printresual(0);//输出结果 mnet.forwardPropagation(mNumImg[1].inputdata); mnet.printresual(0);
运行结果如下:
C++实现 因为网络结构都没有改,改的只是各层节点的个数,前面提到的一些注意点,因此如果对整套代码有不明白的地方可以移步前两篇文章或看看本篇前面提到的5个注意点。
setting.h 1 2 3 4 5 6 7 8 #pragma once #include "time.h" #include <iostream> using namespace std; #define IPNNUM 784 #define HDNNUM 100 #define OPNNUM 10
net.hpp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 #pragma once #include "setting.h" class node { public: double value; //数值,存储结点最后的状态 double *W = NULL; //结点到下一层的权值 void initNode(int num);//初始化函数,必须调用以初始化权值个数 ~node(); //析构函数,释放掉权值占用内存 }; void node::initNode(int num) { W = new double[num]; srand((unsigned)time(NULL)); for (size_t i = 0; i < num; i++)//给权值赋一个随机值 { W[i] = rand() % 100 / double(100)*0.1; if (rand() % 2) { W[i] = -W[i]; } } } node::~node() { if (W != NULL) { delete[]W; } } //网络类,描述神经网络的结构并实现前向传播以及后向传播 class net { public: node inlayer[IPNNUM]; //输入层 node hidlayer[HDNNUM];//隐含层 node outlayer[OPNNUM];//输出层 double yita = 0.1;//学习率η double k1;//输入层偏置项权重 double k2;//隐含层偏置项权重 double Tg[OPNNUM];//训练目标 double O[OPNNUM];//网络实际输出 net();//构造函数,用于初始化各层和偏置项权重 double sigmoid(double z);//激活函数 double getLoss();//损失函数,输入为目标值 void forwardPropagation(double *input);//前向传播,输入为输入层节点的值 void backPropagation(double *T);//反向传播,输入为目标输出值 void printresual(int trainingTimes);//打印信息 }; net::net() { //初始化输入层和隐含层偏置项权值,给一个随机值 srand((unsigned)time(NULL)); k1 = rand() % 100 / double(100); k2 = rand() % 100 / double(100); //初始化输入层到隐含层节点权重 for (size_t i = 0; i < IPNNUM; i++) { inlayer[i].initNode(HDNNUM); } //初始化隐含层到输出层节点权重 for (size_t i = 0; i < HDNNUM; i++) { hidlayer[i].initNode(OPNNUM); } } //激活函数 double net::sigmoid(double z) { return 1 / (1 + exp(-z)); } //损失函数 double net::getLoss() { double mloss = 0; for (size_t i = 0; i < OPNNUM; i++) { mloss += pow(O[i] - Tg[i], 2); } return mloss / OPNNUM; } //前向传播 void net::forwardPropagation(double *input) { for (size_t iNNum = 0; iNNum < IPNNUM; iNNum++)//输入层节点赋值 { inlayer[iNNum].value = input[iNNum]; } for (size_t hNNum = 0; hNNum < HDNNUM; hNNum++)//算出隐含层结点的值 { double z = 0; for (size_t iNNum = 0; iNNum < IPNNUM; iNNum++) { z += inlayer[iNNum].value*inlayer[iNNum].W[hNNum]; } z += k1;//加上偏置项 hidlayer[hNNum].value = sigmoid(z); } for (size_t oNNum = 0; oNNum < OPNNUM; oNNum++)//算出输出层结点的值 { double z = 0; for (size_t hNNum = 0; hNNum < HDNNUM; hNNum++) { z += hidlayer[hNNum].value*hidlayer[hNNum].W[oNNum]; } z += k2;//加上偏置项 O[oNNum] = outlayer[oNNum].value = sigmoid(z); } } //反向传播,这里为了公式好看一点多写了一些变量作为中间值 //计算过程用到的公式在博文中已经推导过了,如果代码没看明白请看看博文 void net::backPropagation(double *T) { for (size_t i = 0; i < OPNNUM; i++) { Tg[i] = T[i]; } for (size_t iNNum = 0; iNNum < IPNNUM; iNNum++)//更新输入层权重 { for (size_t hNNum = 0; hNNum < HDNNUM; hNNum++) { double y = hidlayer[hNNum].value; double loss = 0; for (size_t oNNum = 0; oNNum < OPNNUM; oNNum++) { loss += (O[oNNum] - Tg[oNNum])*O[oNNum] * (1 - O[oNNum])*hidlayer[hNNum].W[oNNum]; } inlayer[iNNum].W[hNNum] -= yita * loss*y*(1 - y)*inlayer[iNNum].value; } } for (size_t hNNum = 0; hNNum < HDNNUM; hNNum++)//更新隐含层权重 { for (size_t oNNum = 0; oNNum < OPNNUM; oNNum++) { hidlayer[hNNum].W[oNNum] -= yita * (O[oNNum] - Tg[oNNum])* O[oNNum] * (1 - O[oNNum])*hidlayer[hNNum].value; } } } void net::printresual(int trainingTimes) { double loss = getLoss(); cout << "训练次数:" << trainingTimes << endl; cout << "loss:" << loss << endl; for (size_t oNNum = 0; oNNum < OPNNUM; oNNum++) { cout << "输出" << oNNum + 1 << ":" << O[oNNum] << endl; } }
getImg.hpp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 #pragma once #include "setting.h" class ImgData//单张图像 { public: unsigned char tag; double data[IPNNUM]; double label[OPNNUM]; }; class getImg { public: ImgData* mImgData; void imgTrainDataRead(const char *datapath, const char *labelpath); ~getImg(); }; void getImg::imgTrainDataRead(const char *datapath, const char *labelpath) { /***********读取图片数据***********/ unsigned char readbuf[4];//信息数据读取空间 FILE *f; fopen_s(&f, datapath, "rb"); fread_s(readbuf, 4, 1, 4, f);//读取魔数,即文件标志位 fread_s(readbuf, 4, 1, 4, f);//读取数据集图像个数 int sumOfImg = (readbuf[0] << 24) + (readbuf[1] << 16) + (readbuf[2] << 8) + readbuf[3];//图像个数 fread_s(readbuf, 4, 1, 4, f);//读取数据集图像行数 int imgheight = (readbuf[0] << 24) + (readbuf[1] << 16) + (readbuf[2] << 8) + readbuf[3];//图像行数 fread_s(readbuf, 4, 1, 4, f);//读取数据集图像列数 int imgwidth = (readbuf[0] << 24) + (readbuf[1] << 16) + (readbuf[2] << 8) + readbuf[3];//图像列数 mImgData = new ImgData[sumOfImg]; unsigned char *data = new unsigned char[IPNNUM]; for (int i = 0; i < sumOfImg; i++) { fread_s(data, IPNNUM, 1, IPNNUM, f);//读取数据集图像列数 for (size_t px = 0; px < IPNNUM; px++)//图像数据归一化 { mImgData[i].data[px] = data[px]/(double)255*0.99+0.01; } } delete[]data; fclose(f); /**********************************/ /***********读取标签数据***********/ /**********************************/ fopen_s(&f, labelpath, "rb"); fread_s(readbuf, 4, 1, 4, f);//读取魔数,即文件标志位 fread_s(readbuf, 4, 1, 4, f);//读取数据集图像个数 sumOfImg = (readbuf[0] << 24) + (readbuf[1] << 16) + (readbuf[2] << 8) + readbuf[3];//图像个数 for (int i = 0; i < sumOfImg; i++) { fread_s(&mImgData[i].tag, 1, 1, 1, f);//读取数据集图像列数 for (size_t j = 0; j < 10; j++) { mImgData[i].label[j] = 0.01; } mImgData[i].label[mImgData[i].tag] = 0.99; } fclose(f); } getImg::~getImg() { delete[]mImgData; }
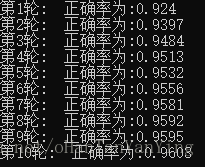
BPNetC.cpp 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 #include "setting.h" #include "net.hpp"//神经网络 #include "getImg.hpp"//训练数据 void AccuracyRate(int time, net *mnet, getImg *mImg)//精确率评估 { double tagright = 0;//正确个数统计 for (size_t count = 0; count < 10000; count++) { mnet->forwardPropagation(mImg->mImgData[count].data);//前向传播 double value = -100; int gettag = -100; for (size_t i = 0; i < 10; i++) { if (mnet->outlayer[i].value > value) { value = mnet->outlayer[i].value; gettag = i; } } if (mImg->mImgData[count].tag == gettag) { tagright++; } } //mnet.printresual(0);//信息打印 cout << "第" << time + 1 << "轮: "; cout << "正确率为:" << tagright / 10000 << endl; } int main() { getImg mGetTrainImg; mGetTrainImg.imgTrainDataRead("train-images.idx3-ubyte", "train-labels.idx1-ubyte"); getImg mGetTestImg; mGetTestImg.imgTrainDataRead("t10k-images.idx3-ubyte", "t10k-labels.idx1-ubyte"); net mnet;//神经网络对象 for (size_t j = 0; j < 10; j++) { for (size_t i = 0; i < 60000; i++) { mnet.forwardPropagation(mGetTrainImg.mImgData[i].data);//前向传播 mnet.backPropagation(mGetTrainImg.mImgData[i].label);//反向传播 } AccuracyRate(j,&mnet, &mGetTestImg); } std::cout << "搞完收工!\n"; }
python实现 距离C++第一个版本完成过去了有半年多了,因为入学后各种事情搞得分身乏术,剩下一点时间也用来打游戏调解了哈哈哈。研究需要!!! 又开始看神经网络,因此顺便修改了C++的第一个版本,并且把python版本也做了出来。万万没想到之前写的版本有bug,调了一天才调通了,看了之前文章python代码的同志们实在是抱歉!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 import numpy as np import struct def loadImageSet(filename): print ("load image set",filename) binfile= open(filename, 'rb') buffers = binfile.read() head = struct.unpack_from('>IIII' , buffers ,0) print ("head,",head) offset = struct.calcsize('>IIII') imgNum = head[1] width = head[2] height = head[3] #[60000]*28*28 bits = imgNum * width * height bitsString = '>' + str(bits) + 'B' #读取定长数据段,即字符集图片总和 imgs = struct.unpack_from(bitsString,buffers,offset) binfile.close() imgs = np.reshape(imgs,[imgNum,1,width*height])#将字符集图片分隔为单张图片 print ("load imgs finished") return imgs def loadLabelSet(filename): print ("load label set",filename) binfile = open(filename, 'rb') buffers = binfile.read() head = struct.unpack_from('>II' , buffers ,0) print ("head,",head) imgNum=head[1] offset = struct.calcsize('>II') numString = '>'+str(imgNum)+"B" labels = struct.unpack_from(numString , buffers , offset) binfile.close() labels = np.reshape(labels,[imgNum,1]) print ('load label finished') return labels
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 import ReadData as rd import matplotlib.pyplot as plt import math import random import numpy as np IPNNUM=784 #输入层节点数 HDNNUM=100 #隐含层节点数 OPNNUM=10 #输出层节点数 class node: #结点类,用以构成网络 def __init__(self,connectNum=0): self.value=0 #数值,存储结点最后的状态,对应到文章示例为X1,Y1等值 self.W = (2*np.random.random_sample(connectNum)-1)*0.01 class net: #网络类,描述神经网络的结构并实现前向传播以及后向传播 def __init__(self): #初始化函数,用于初始化各层间节点和偏置项权重 #输入层结点 self.inlayer=[node(HDNNUM)]; for obj in range(1, IPNNUM): self.inlayer.append(node(HDNNUM)) #隐含层结点 self.hidlayer=[node(OPNNUM)]; for obj in range(1, HDNNUM): self.hidlayer.append(node(OPNNUM)) #输出层结点 self.outlayer=[node(0)]; for obj in range(1, OPNNUM): self.outlayer=[node(0)] self.yita = 0.1 #学习率η self.k1=random.random() #输入层偏置项权重 self.k2=random.random() #隐含层偏置项权重 self.Tg=np.zeros(OPNNUM) #训练目标 self.O=np.zeros(OPNNUM) #网络实际输出 def sigmoid(self,z): #激活函数 return 1 / (1 + math.exp(-z)) def getLoss(self): #损失函数 loss=0 for num in range(0, OPNNUM): loss+=pow(self.O[num] -self.Tg[num],2) return loss/OPNNUM def forwardPropagation(self,input): #前向传播 for i in range(0, IPNNUM): #输入层节点赋值 self.inlayer[i].value = input[i] for hNNum in range(0,HDNNUM): #算出隐含层结点的值 z = 0 for iNNum in range(0,IPNNUM): z+=self.inlayer[iNNum].value*self.inlayer[iNNum].W[hNNum] #加上偏置项 z+= self.k1 self.hidlayer[hNNum].value = self.sigmoid(z) for oNNum in range(0,OPNNUM): #算出输出层结点的值 z = 0 for hNNum in range(0,HDNNUM): z += self.hidlayer[hNNum].value* self.hidlayer[hNNum].W[oNNum] z += self.k2 self.O[oNNum] = self.sigmoid(z) def backPropagation(self,T): #反向传播,这里为了公式好看一点多写了一些变量作为中间值 for num in range(0, OPNNUM): self.Tg[num] = T[num] for iNNum in range(0,IPNNUM): #更新输入层权重 for hNNum in range(0,HDNNUM): y = self.hidlayer[hNNum].value loss = 0 for oNNum in range(0, OPNNUM): loss+=(self.O[oNNum] - self.Tg[oNNum])*self.O[oNNum] * (1 - self.O[oNNum])*self.hidlayer[hNNum].W[oNNum] self.inlayer[iNNum].W[hNNum] -= self.yita*loss*y*(1- y)*self.inlayer[iNNum].value for hNNum in range(0,HDNNUM): #更新隐含层权重 for oNNum in range(0,OPNNUM): self.hidlayer[hNNum].W[oNNum]-= self.yita*(self.O[oNNum] - self.Tg[oNNum])*self.O[oNNum]*\ (1- self.O[oNNum])*self.hidlayer[hNNum].value def printresual(self,trainingTimes): #信息打印 loss = self.getLoss() print("训练次数:", trainingTimes) print("loss",loss) for oNNum in range(0,OPNNUM): print("输出",oNNum,":",self.O[oNNum]) #主程序 mnet=net() imgs=rd.loadImageSet("train-images.idx3-ubyte"); labels=rd.loadLabelSet("train-labels.idx1-ubyte"); ##显示图像 #im=np.array(input) #im = im.reshape(28,28) #fig = plt.figure() #plotwindow = fig.add_subplot(111) #plt.imshow(im , cmap='gray') #plt.show() for n in range(0,1000): print(n) for x in range(0,3): input=(imgs[x,:]/255*0.99+0.01).ravel() #ravel多维转1维 target=np.ones(10)*0.01 target[labels[x]]=0.99 mnet.forwardPropagation(input) mnet.backPropagation(target) if (n%200==0): mnet.printresual(n)
pytorch的CPU实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 # coding=utf-8 import time import torch import torch.nn as nn from torch.autograd import Variable import torchvision.datasets as dsets import torchvision.transforms as transforms #网络模型 class Net(nn.Module): def __init__(self): #定义Net的初始化函数,这个函数定义了该神经网络的基本结构 super(Net, self).__init__() #复制并使用Net的父类的初始化方法,即先运行nn.Module的初始化函数 self.intohid_layer = nn.Linear(784, 100) #定义输入层到隐含层的连结关系函数 self.hidtoout_layer = nn.Linear(100, 10)#定义隐含层到输出层的连结关系函数 def forward(self, input): #定义该神经网络的向前传播函数,该函数必须定义,一旦定义成功,向后传播函数也会自动生成 x = torch.sigmoid(self.intohid_layer(input)) #输入input在输入层经过经过加权和与激活函数后到达隐含层 x = torch.sigmoid(self.hidtoout_layer(x)) #类似上面 return x mnet = Net() #数据集 train_dataset = dsets.MNIST(root = '../mnist/', #选择数据的根目录 train = True, # 选择训练集 transform = transforms.ToTensor(), # 转换成tensor变量 download = False) # 不从网络上download图片 test_dataset = dsets.MNIST(root = '../mnist/', # 选择数据的根目录 train = False, # 选择训练集 transform = transforms.ToTensor(),# 转换成tensor变量 download = False) # 不从网络上download图片 # 加载数据 train_loader = torch.utils.data.DataLoader(dataset = train_dataset, batch_size = 1,#每一次训练选用的数据个数 shuffle = False)#将数据打乱 test_loader = torch.utils.data.DataLoader(dataset = test_dataset, batch_size = 1000,#每一次训练选用的数据个数 shuffle = False) loss_fn = torch.nn.MSELoss()#损失函数定义,可修改 optimizer = torch.optim.SGD(mnet.parameters(), lr = 0.1, momentum=0.9) start = time.time() for epoch in range(1):#训练次数 print('current epoch = %d' % epoch) for i, (images, labels) in enumerate(train_loader): #利用enumerate取出一个可迭代对象的内容 images = Variable(images.view(-1, 28 * 28)) labels = Variable(labels) labels = torch.LongTensor(labels).view(-1,1)#将标签转为单列矩阵 target= torch.zeros(1, 10).scatter_(dim = 1, index = labels, value = 0.98)#将标签转为onehot形式 target+=0.01 optimizer.zero_grad() #清空节点值 outputs = mnet(images) #前向传播 loss = loss_fn(outputs, target) #损失计算 loss.backward() #后向传播 optimizer.step() #更新权值 if i % 10000 == 0: print(i) total = 0 correct = 0.0 for images, labels in test_loader: images = Variable(images.view(-1, 28 * 28)) outputs = mnet(images) #前向传播 _, predicts = torch.max(outputs.data, 1) #返回预测结果 total += labels.size(0) correct += (predicts == labels).sum() print('Accuracy = %.2f' % (100 * float(correct) / total)) end = time.time() print('花费时间%.2f' % (end - start))
上面的代码在频率为3.40GHz的电脑上,训练10遍,每次都遍历一整个训练集要花费1000s左右,也就是16.7分钟左右,因全连接神经网络的过拟合问题,正确率基本到了97.5%之后就再也升不上去了。
pytorch的GPU实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 # coding=utf-8 import time import torch import torch.nn as nn from torch.autograd import Variable import torchvision.datasets as dsets import torchvision.transforms as transforms #网络模型 class Net(nn.Module): def __init__(self): #定义Net的初始化函数,这个函数定义了该神经网络的基本结构 super(Net, self).__init__() #复制并使用Net的父类的初始化方法,即先运行nn.Module的初始化函数 self.intohid_layer = nn.Linear(784, 100) #定义输入层到隐含层的连结关系函数 self.hidtoout_layer = nn.Linear(100, 10)#定义隐含层到输出层的连结关系函数 def forward(self, input): #定义该神经网络的向前传播函数,该函数必须定义,一旦定义成功,向后传播函数也会自动生成 x = torch.sigmoid(self.intohid_layer(input)) #输入input在输入层经过经过加权和与激活函数后到达隐含层 x = torch.sigmoid(self.hidtoout_layer(x)) #类似上面 return x mnet = Net().cuda() #数据集 train_dataset = dsets.MNIST(root = '../mnist/', #选择数据的根目录 train = True, # 选择训练集 transform = transforms.ToTensor(), # 转换成tensor变量 download = False) # 不从网络上download图片 test_dataset = dsets.MNIST(root = '../mnist/', # 选择数据的根目录 train = False, # 选择训练集 transform = transforms.ToTensor(),# 转换成tensor变量 download = False) # 不从网络上download图片 # 加载数据 train_loader = torch.utils.data.DataLoader(dataset = train_dataset, batch_size = 1,#每一次训练选用的数据个数 shuffle = False)#将数据打乱 test_loader = torch.utils.data.DataLoader(dataset = test_dataset, batch_size = 1000,#每一次训练选用的数据个数 shuffle = False) loss_fn = torch.nn.MSELoss()#损失函数定义,可修改 optimizer = torch.optim.SGD(mnet.parameters(), lr = 0.1, momentum=0.9) start = time.time() for epoch in range(1):#训练次数 print('current epoch = %d' % epoch) for i, (images, labels) in enumerate(train_loader): #利用enumerate取出一个可迭代对象的内容 images = Variable(images.view(-1, 28 * 28).cuda()) labels = Variable(labels.cuda()) labels = torch.cuda.LongTensor(labels).view(-1,1)#将标签转为单列矩阵 target= torch.zeros(1, 10).cuda().scatter_(dim = 1, index = labels, value = 0.98)#将标签转为onehot形式 target+=0.01 optimizer.zero_grad() #清空节点值 outputs = mnet(images) #前向传播 loss = loss_fn(outputs, target) #损失计算 loss.backward() #后向传播 optimizer.step() #更新权值 if i % 10000 == 0: print(i) total = 0 correct = 0.0 for images, labels in test_loader: images = Variable(images.view(-1, 28 * 28).cuda()) outputs = mnet(images) #前向传播 _, predicts = torch.max(outputs.data, 1) #返回预测结果 total += labels.size(0) correct += (predicts == labels.cuda()).sum() print('Accuracy = %.2f' % (100 * float(correct) / total)) end = time.time() print('花费时间%.2f' % (end - start))
另外写文章累人,写代码掉头发,如果觉得文章有帮助,哈哈哈