深度学习1---最简单的全连接神经网络

本文有一部分内容参考以下两篇文章：
　　一文弄懂神经网络中的反向传播法——BackPropagation
　　神经网络
　　
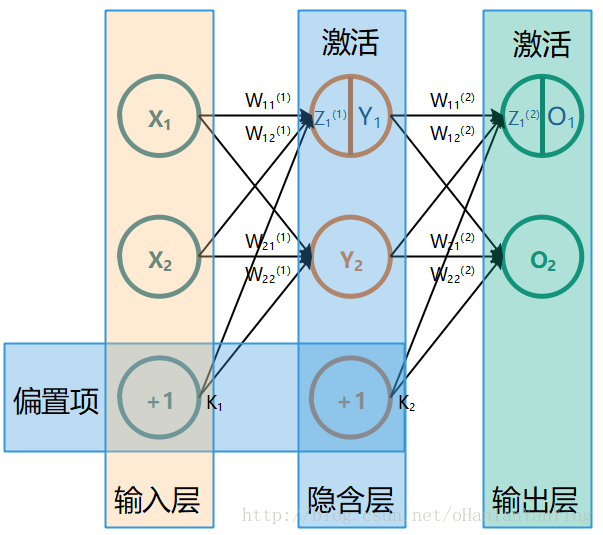
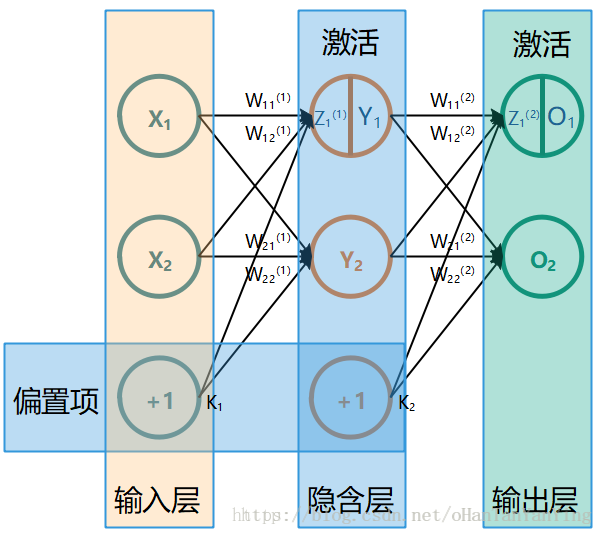
　　最简单的全连接神经网络如下图所示(这张图极其重要，本文所有的推导都参照的这张图，如果有兴趣看推导，建议保存下来跟推导一起看)：

这里写图片描述

　　它的前向传播计算过程非常简单，这里先讲一下：

前向传播

$$
\begin{aligned}
Y_{1} &=f\left(W_{11}^{(1)} X_{1}+W_{12}^{(1)} X_{2}+K_{1}\right) \
Y_{2} &=f\left(W_{21}^{(1)} X_{1}+W_{22}^{(1)} X_{2}+K_{1}\right) \
O_{1} &=f\left(W_{11}^{(2)} Y_{1}+W_{12}^{(2)} Y_{2}+K_{2}\right) \
O_{2} &=f\left(W_{21}^{(2)} Y_{1}+W_{22}^{(2)} Y_{2}+K_{2}\right)
\end{aligned}
$$
　　具体的，如果代入实际数值，取
$$
\begin{array}{lc}
X_{1}=0.05 & X_{2}=0.10 \
K_{1}=0.35 & K_{2}=0.60 \
W_{11}^{(1)}=0.15 & W_{12}^{(1)}=0.20 \
W_{21}^{(1)}=0.25 & W_{22}^{(1)}=0.30 \
W_{11}^{(2)}=0.40 & W_{12}^{(2)}=0.45 \
W_{21}^{(2)}=0.50 & W_{22}^{(2)}=0.55
\end{array}
$$

　　激活函数为：
$$
\frac{1}{1+e^{-z}}
$$
　　则有：
$$
\begin{array}{l}
z_{1}^{(1)}=0.15 * 0.05+0.20 * 0.10+0.35=0.3775 \
Y_{1}=\frac{1}{1+e^{-z_{1}^{(1)}}}=\frac{1}{1+e^{-0.3775}}=0.5932699921 \
z_{2}^{(1)}=0.25 * 0.05+0.30 * 0.10+0.35=0.3925 \
Y_{2}=\frac{1}{1+e^{-z_{2}^{(1)}}}=\frac{1}{1+e^{-0.3925}}=0.5968843783 \
z_{1}^{(2)}=0.40 * 0.5932699921+0.45 * 0.5968843783+0.60=1.1059059671 \
O_{1}=\frac{1}{1+e^{-z_{2}^{(2)}}}=\frac{1}{1+e^{-1.1059059671}}=0.7513650696 \
z_{2}^{(2)}=0.50 * 0.5932699921+0.55 * 0.5968843783+0.60=1.2249214041 \
O_{2}=\frac{1}{1+e^{-z_{2}^{(2)}}}=f(1.2249214041)=\frac{1}{1+e^{-1.2249210041}}=0.7729284653
\end{array}
$$

　　经过上面的过程，我们就完成了一次神经网络从输入到输出的计算。虽然公式代入数值看起来比较要命，但实际上对于计算机来说并没有什么。
　　那它有什么用呢？单看上面的例子可以说是完全没用的，因为它的输出跟输入的关系还非常的模糊。我们需要做的是训练这个网络中的参数，使得输出和输入存在某种对应关系（比如输入1、1，输出1、0来实现一个类似于加法器这样的东西），当上面网络的参数训练好了，我们工程中就只需要将数据输入这个网络，然后看看输出结果就行。从这里也大致可以看到，神经网络在实际应用中计算量大归大（可能网络本身就很复杂），但其实也还可以接受，最要命的地方是在于训练(每训练一次都要做一次前向传播计算，一般训练的次数又是以万为单位的)！
　　以上面的网络为例，通常我们说的训练参数就是训练公式中跟W相关的那8个数。在具体展开讲之前先补充下上面用到的神经网络的两个知识点：

激活函数，也就是上面例子中的
　　$$
\frac{1}{1+e^{-z}}
$$
（事实上只要满足一定的规范，激活函数可以有无数种形态，不一定就用这个），其大体有两个作用：
1.将数据归一化，因为前一层网络的计算结果很有可能不在0~1之间，而数据的范围需要统一，因此用激活函数把数据范围给限定住。
　　2.打破网络的线性映射关系，如果网络只存在线性关系，则无论网络多深多复杂，最后都可以用单层网络替换，这样也就跟深度学习没什么关系了。另外更重要的一点是，如果只有线性，对于非线性的数据要分类是无能为力的。
偏置项，也就是本篇最开始的网络图中最底层的那个“+1”
　　对这个东西有什么用，有些解释如下：
　　Y=WX+b （1）
　　假设没有b，则公式退化成
　　Y=WX （2）
　　假设现在要把(1,1)、(2,2)这两个点分成不同的类，则公式（2）直接就跪了，而公式（1）可以做到。
　　但，本人不同意这个说法，因为这样的话(1,b)、(2,b)这两个点就分不出来了。也就是说按照这样的解释方法加入偏置项虽然能解决一部分问题，但会带入另外的问题，并没有什么卵用。
　　本人对偏置项作用的看法是，偏置项要结合激活函数来看，每一层网络虽然共享一个偏置项，然而因为前面计算的结果有所差异（如例子中
$$
W_{11}^{(1)} X_{1}+W_{12}^{(1)} X_{2}与 W_{21}^{(1)} X_{1}+W_{22}^{(1)} X_{2}
$$
)，而激活函数又非线性函数，因而可以将神经元较快的分化出来。

反向传播

　　承接上面，我们来讲最重要的参数训练问题，深度学习一般用反向传播法更新权重(甚至可以说反向传播是神经网络的灵魂)。它的作用其实很好理解，下面结合着上面举的例子解释一下。

上面我们的输入是：
$$
X_{1}=0.05 \quad X_{2}=0.10
$$

　　对应的输出是：
　　
$$
O_{1}=0.7513650696 \quad O_{2}=0.7729284653
$$
　　假设我们希望输入对应的输出为：
$$
O_{1}=0.01 \quad O_{2}=0.99
$$
　　我们就需要改变Ｗ的取值，而具体要改变多少，我们一般会用梯度下降的方法去评估。在讲梯度下降之前，先来看看评价误差大小的“损失函数”。
　　 损失函数，也叫做“代价函数”，损失函数越小，就代表模型拟合的越好。最常用的损失函数是均方误差：
　　
$$
E_{\text {总 }}=\frac{\sum_{i=1}^{n}\left(T_{i}-O_{i}\right)^{2}}{n}(其中T_{i}为期望网络输出的结果，T_{i}为实际网络输出的结果)
$$
　　代入上面例子的期望输出和实际输出数值则可以求得
　　
$$
E_{\text {总 }}=\frac{\sum_{i=1}^{n}\left(T_{i}-O_{i}\right)^{2}}{n}=E_{O_{1}}+E_{O_{2}}=\frac{(0.01-0.7513650696)^{2}}{2}+\frac{(0.99-0.7729284653)^{2}}{2}
$$
　　通过损失函数算出误差大小之后我们就可以大概知道网络训练的怎么样了，是不是已经大致能工作之类的。
　　OK，下面进入梯度下降法：
　　梯度下降法
　　要求单个的W对于总体误差起到多大的影响。在数学上，就是求总体误差对相应W的偏导数。以示例中隐含层到输出层的
$$
W_{11}^{(2)} 为例, 就是求 \frac{\partial E_{总}}{\partial W_{11}^{(2)}} 。
$$
要直接求基本是不可能的，我们可以先分析下
$$
W_{11}^{(2)} 到 E_{\text {总 }}
$$
间到底经历了什么。
$$

W_{11}^{(2)} 先与 Y_{1} 相乘
$$

W(2)11W11(2)先与Y1Y1相乘
经过激活函数

　　3. 经过误差计算公式，也就是损失函数

因此我们可以把
$$
\frac{\partial E_{总}}{\partial W_{11}^{(2)}}
$$
拆开来（链式法则，高数学的不好的同学回去翻书），如下：
$$
\frac{\partial E_{兄}}{\partial W_{11}^{(2)}}=\frac{\partial E_{兄}}{\partial O_{1}} * \frac{\partial O_{1}}{\partial z_{1}^{(2)}} * \frac{\partial z_{1}^{(2)}}{\partial W_{11}^{(2)}} \quad\left(z_{1}^{(2)} \text { 为经过激活函数前的状态 }\right)
$$
　　这样，只要能分别求出这三个部分，整体也就求出来了。
　　下面先列出被微分的这几项
$$
\begin{array}{l}
E_{\text {总 }}=E_{O_{1}}+E_{O_{2}}=\frac{\left(T_{1}-O_{1}\right)^{2}}{2}+\frac{\left(T_{2}-O_{2}\right)^{2}}{2} \
O_{1}=\frac{1}{1+e^{-z_{1}^{(2)}}} \
z_{1}^{(2)}=W_{11}^{(2)} Y_{1}+W_{12}^{(2)} Y_{2}+K_{2}
\end{array}
$$

　　分别做偏微分得到
$$
\begin{aligned}
\frac{\partial E_{\text {兄 }}}{\partial O_{1}}=\frac{\partial\left[\frac{\left(T_{1}-O_{1}\right)^{2}}{2}+\frac{\left(T_{2}-O_{2}\right)^{2}}{2}\right]}{\partial O_{1}}=-\left(T_{1}-O_{1}\right)=O_{1}-T_{1} \
\frac{\partial O_{1}}{\partial z_{1}^{(2)}}=\frac{\partial \frac{1}{1+e^{-z_{1}^{(2)}}}}{\partial z_{1}^{(2)}}=\frac{e^{-z_{1}^{(2)}}}{\left(1+e^{-z_{1}^{(2)}}\right)^{2}} &=\frac{1+e^{-z_{1}^{(2)}-1}}{\left(1+e^{-z_{1}^{(2)}}\right)^{2}}=\frac{1}{1+e^{-z_{1}^{(2)}}}\left(1-\frac{1}{1+e^{-z_{1}^{(2)}}}\right)=O_{1}\left(1-O_{1}\right) \
\frac{\partial z_{1}^{(2)}}{\partial W_{11}^{(2)}} &=\frac{\partial\left(W_{11}^{(2)} Y_{1}+W_{12}^{(2)} Y_{2}+K_{2}\right)}{\partial W_{11}^{(2)}}=Y_{1}
\end{aligned}
$$

　　代入具体数值得到
$$
\begin{array}{l}
\frac{\partial E_{\text {总 }}}{\partial O_{1}}=O_{1}-T_{1}=0.7513650696-0.01=0.7413650696 \
\frac{\partial O_{1}}{\partial z_{1}^{(2)}}=O_{1}\left(1-O_{1}\right)=0.7513650695(1-0.7513650695)=0.1868156018 \
\frac{\partial z_{1}^{(2)}}{\partial W_{11}^{(2)}}=Y_{1}=0.5932699921 \
\text { 则 } \frac{\partial E_{\text {总 }}}{\partial W_{11}^{(2)}}=\frac{\partial E_{\text {总 }}}{\partial O_{1}} * \frac{\partial O_{1}}{\partial z_{1}^{(2)}} * \frac{\partial z_{1}^{(2)}}{\partial W_{11}^{(2)}}=\left(O_{1}-T_{1}\right) * O_{1}\left(1-O_{1}\right) * Y_{1}=0.7413650696 \
\quad * 0.1868156018 * 0.5932699921=0.0821670406
\end{array}
$$

　　到此，我们求出了总体误差对相应隐含层的权重W的偏导数。他的含义是在当前位置上，如果权重W移动一小段距离，会引起总体误差的变化的大小。很容易可以想到，如果求出来的值比较大，证明该权重对误差的影响大，那么我们需要对它调整的步伐也就大。反之，则稍微调整一下就可以了。调整的公式如下：
$$
W_{n e w 11}^{(2)}=W_{11}^{(2)}-\eta * \frac{\partial E_{总}}{\partial W_{11}^{(2)}}
$$
　　公式中的η为学习速率，这哥们比较关键，如果取得太大有可能怎么训练都无法取得最优值，取得太小训练速度又非常的慢，且很容易就会陷入局部最优而出不来，关于这块的解释可以参考机器学习的书籍，如果有必要后面会专门出一篇文章来探讨这个问题，本文在示例中取η=0.5。
　　那么，代入数值：
$$
W_{n e w 11}^{(2)}=W_{11}^{(2)}-\eta * \frac{\partial E_{\underline{g}}}{\partial W_{11}^{(2)}}=0.40-0.5 * 0.0821670406=0.3589164797
$$

　　　　有了上面的推导，更新隐含层剩下的三个权重可以说易如反掌：
$$
　　\begin{array}{l}
　　W_{\text {new} 12}^{(2)}=0.45-0.5 *\left(O_{1}-T_{1}\right) * O_{1}\left(1-O_{1}\right) * Y_{2}=0.4086661861 \
　　W_{\text {new} 21}^{(2)}=0.50-0.5 *\left(O_{2}-T_{2}\right) * O_{2}\left(1-O_{2}\right) * Y_{1}=0.5113012703 \
　　W_{\text {new} 22}^{(2)}=0.55-0.5 *\left(O_{2}-T_{2}\right) * O_{2}\left(1-O_{2}\right) * Y_{2}=0.5613701211
　　\end{array}
$$

　　　　接下来还有输入层到隐含层的权重，基本原理是一样的，但因为所处位置比较前，所有改变这个位置的一个权重会影响两个输出的值，求偏导也要考虑两个输出的影响。
$$
　　\frac{\partial E_{\text {总 }}}{\partial W_{11}^{(1)}}=\frac{\partial E_{\text {总 }}}{\partial Y_{1}} * \frac{\partial Y_{1}}{\partial z_{1}^{(1)}} * \frac{\partial z_{1}^{(1)}}{\partial W_{11}^{(1)}}
$$

　　　　可以看到，后面两项跟隐含层到输出层的偏导几乎一模一样，可以套用其结论，公式变为：
$$
　　\frac{\partial E_{\text {总 }}}{\partial W_{11}^{(1)}}=\frac{\partial E_{\text {总 }}}{\partial Y_{1}} * Y_{1}\left(1-Y_{1}\right) * X_{1}
$$

　　　　现在主要就要求
$$
　　\frac{\partial E_{\text {总 }}}{\partial Y_{1}}，
$$
　　回头看本文一开始的图片，可以看到E总和Y1的距离是比较远的，无法直接求偏导，因而需要通过链式法则再展开一下。
　　　　
$$
　　\frac{\partial E_{\text {总 }}}{\partial Y_{1}}=\frac{\partial\left(E_{O_{1}}+E_{O_{2}}\right)}{\partial Y_{1}}=\frac{\partial E_{O_{1}}}{\partial Y_{1}}+\frac{\partial E_{O_{2}}}{\partial Y_{1}}
$$

　　　　因为
$$
　　\frac{\partial E_{O_{1}}}{\partial Y_{1}}与\frac{\partial E_{O_{2}}}{\partial Y_{1}}
$$
　　形式相同，因而先看前者。
　　　　
$$
　　\frac{\partial E_{O_{1}}}{\partial Y_{1}}=\frac{\partial E_{O_{1}}}{\partial O_{1}} * \frac{\partial O_{1}}{\partial z_{1}^{(2)}} * \frac{\partial z_{1}^{(2)}}{\partial Y_{1}}
$$

　　　　前面两项之前求过，因此上式变成：
$$
　　\frac{\partial E_{O_{1}}}{\partial Y_{1}}=\frac{\partial E_{O_{1}}}{\partial O_{1}} * \frac{\partial O_{1}}{\partial z_{1}^{(2)}} * \frac{\partial z_{1}^{(2)}}{\partial Y_{1}}=\left(O_{1}-T_{1}\right) * O_{1}\left(1-O_{1}\right) * \frac{\partial z_{1}^{(2)}}{\partial Y_{1}}
$$
　　又
$$
　　\frac{\partial z_{1}^{(2)}}{\partial Y_{1}}=\frac{\partial\left(W_{11}^{(2)} Y_{1}+W_{12}^{(2)} Y_{2}+K_{2}\right)}{\partial Y_{1}}=W_{11}^{(2)}
$$

　　　　故
$$
　　\frac{\partial E_{O_{1}}}{\partial z_{1}^{(1)}}=\left(O_{1}-T_{1}\right) * O_{1}\left(1-O_{1}\right) * W_{11}^{(2)}
$$

　　　　同理
$$
　　\frac{\partial E_{O_{2}}}{\partial z_{1}^{(1)}}=\left(O_{2}-T_{2}\right) * O_{2}\left(1-O_{2}\right) * W_{21}^{(2)}
$$

　　　　则
$$
　　\frac{\partial E_{总}}{\partial W_{11}^{(1)}}=\left(\left(O_{1}-T_{1}\right) * O_{1}\left(1-O_{1}\right) * W_{11}^{(2)}+\left(O_{2}-T_{2}\right) * O_{2}\left(1-O_{2}\right) * W_{21}^{(2)}\right)* Y_{1}\left(1-Y_{1}\right) * X_{1}
$$

　　　　代入数值可求得
　　　　
$$
　　\frac{\partial E_{总}}{\partial W_{11}^{(1)}}=0.000438568
$$

　　　　则参数更新为
　　　　
$$
　　\begin{aligned}
　　&W_{n e w 11}^{(1)}=W_{11}^{(1)}-\eta * \frac{\partial E_{总}}{\partial W_{11}^{(1)}}=0.149781\
　　&\text { 同理可求得： }\
　　&W_{n e w 12}^{(1)}=W_{12}^{(1)}-\eta * \frac{\partial E_{总}}{\partial W_{12}^{(1)}}=0.199561\
　　&W_{n e w 21}^{(1)}=W_{21}^{(1)}-\eta * \frac{\partial E_{总}^{(1)}}{\partial W_{21}^{(1)}}=0.249751\
　　&W_{n e w 22}^{(1)}=W_{22}^{(1)}-\eta * \frac{\partial E_{总}^{(1)}}{\partial W_{22}^{(1)}}=0.299502
　　\end{aligned}
$$

　　　　到此，理论部分就都讲完了，万岁！！！

　　在这里在此说明下，本文主要参考一文弄懂神经网络中的反向传播法——BackPropagation这篇文章，里面有些论证直接是按照作者的思路来的，而且代入数据也直接抄的作者的数据，因为这样做本人在写的过程中可以通过比较结果是不是跟它一样来验证推导出的公式正确与否。如果觉得本人写的还不是太清楚可以看看该文章，作者用了比较多的图片辅助解释可能会比较易懂(本人都集中到一张图中了)。
　　在这里顺便推荐一下该作者的博客，写的很好！一看作者说自己只是本科生，我觉得我研究生白读了，额。。。

C++实现

　　直接上代码

#include <iostream>#include <cmath>using namespace std;//结点类，用以构成网络class node 
{public:    double value; //数值，存储结点最后的状态，对应到文章示例为X1，Y1等值    double W[2];  //结点到下一层的权值};//网络类，描述神经网络的结构并实现前向传播以及后向传播//这里为文章示例中的三层网络，每层结点均为两个class net 
{public:
    node input_layer[2];//输入层结点
    node hidden_layer[2];//隐含层结点
    node output_layer[2];//输出层结点,这里只是两个数，但这样做方便后面的扩展    double yita = 0.5;//学习率η    double k1;//输入层偏置项权重    double k2;//隐含层偏置项权重    double Tg[2];//训练目标    double O[2];//网络实际输出

    net();//构造函数，用于初始化权重，一般可以随机初始化    double sigmoid(double z);//激活函数    double getLoss();//损失函数，输入为目标值    void forwardPropagation(double input1,double input2);//前向传播    void backPropagation(double T1, double T2);//反向传播，更新权值    void printresual();//打印信息};

net::net()
{
    k1 = 0.35;
    k2 = 0.60;
    input_layer[0].W[0] = 0.15;
    input_layer[0].W[1] = 0.25;
    input_layer[1].W[0] = 0.20;
    input_layer[1].W[1] = 0.30;
    hidden_layer[0].W[0] = 0.40;
    hidden_layer[0].W[1] = 0.50;
    hidden_layer[1].W[0] = 0.45;
    hidden_layer[1].W[1] = 0.55;
}//激活函数double net::sigmoid(double z)
{    return 1/(1+ exp(-z));
}//损失函数double net::getLoss()
{    return (pow(O[0] -Tg[0],2)+ pow(O[1] - Tg[1],2))/2;
}//前向传播void net::forwardPropagation(double input1, double input2)
{
    input_layer[0].value = input1;
    input_layer[1].value = input2;    for (size_t hNNum = 0; hNNum < 2; hNNum++)//算出隐含层结点的值
    {        double z = 0;        for (size_t iNNum = 0; iNNum < 2; iNNum++)
        {
            z+= input_layer[iNNum].value*input_layer[iNNum].W[hNNum];
        }
        z+= k1;//加上偏置项
        hidden_layer[hNNum].value = sigmoid(z);
    }    for (size_t outputNodeNum = 0; outputNodeNum < 2; outputNodeNum++)//算出输出层结点的值
    {        double z = 0;        for (size_t hNNum = 0; hNNum < 2; hNNum++)
        {
            z += hidden_layer[hNNum].value*hidden_layer[hNNum].W[outputNodeNum];
        }
        z += k2;//加上偏置项
        O[outputNodeNum] = output_layer[outputNodeNum].value = sigmoid(z);
    }
}//反向传播，这里为了公式好看一点多写了一些变量作为中间值//计算过程用到的公式在博文中已经推导过了，如果代码没看明白请看看博文void net::backPropagation(double T1, double T2)
{   
    Tg[0] = T1;
    Tg[1] = T2;    for (size_t iNNum = 0; iNNum < 2; iNNum++)//更新输入层权重
    {        for (size_t wnum = 0; wnum < 2; wnum++)
        {            double y = hidden_layer[wnum].value;
            input_layer[iNNum].W[wnum] -= yita*((O[0] - T1)*O[0] *(1- O[0])*
                hidden_layer[wnum].W[0] +(O[1] - T2)*O[1] *(1 - O[1])*hidden_layer[wnum].W[1])*
                y*(1- y)*input_layer[iNNum].value;
        }
    }    for (size_t hNNum = 0; hNNum < 2; hNNum++)//更新隐含层权重
    {        for (size_t wnum = 0; wnum < 2; wnum++)
        {
            hidden_layer[hNNum].W[wnum]-= yita*(O[wnum] - Tg[wnum])*
                O[wnum] *(1- O[wnum])*hidden_layer[hNNum].value;
        }
    }
}void net::printresual()
{    double loss = getLoss();
    cout << "loss：" << loss << endl;
    cout << "输出1：" << O[0] << endl;
    cout << "输出2：" << O[1] << endl;
}void main()
{
    net mnet;    for (size_t i = 0; i < 10000; i++)
    {
        mnet.forwardPropagation(0.05, 0.1);//前向传播
        mnet.backPropagation(0.01, 0.99);//反向传播        if (i%1000==0)
        {
            mnet.printresual();//反向传播
        }
    }
}

python实现

　　这里本人将贴出自己写的代码，但因为python是初学的，还不太行，所以如有错误和不够简练的地方望请见谅。另外推荐一个网站可以学习各种编程语言的：http://www.runoob.com/python/python-tutorial.html
　　哦哦，上面提到的博文也贴出了博主自行实现的python代码，本人因为初学无法评价，如有兴趣可以去看看。

import mathclass node:    #结点类，用以构成网络    def __init__(self,w1=None,w2=None):
        self.value=0; #数值，存储结点最后的状态，对应到文章示例为X1，Y1等值
        self.W=[w1,w2]; #结点到下一层的权值class net:    #网络类，描述神经网络的结构并实现前向传播以及后向传播    #这里为文章示例中的三层网络，每层结点均为两个    def __init__(self):        #初始化函数，将权重，偏置等值全部初始化为博文示例的数值
        self.inlayer =[node(0.15,0.25),node(0.20,0.30)]; #输入层结点
        self.hidlayer=[node(0.40,0.50),node(0.45,0.55)]; #隐含层结点
        self.outlayer=[node(),node()];                   #输出层结点

        self.yita = 0.5;                                 #学习率η
        self.k1=0.35;                                    #输入层偏置项权重
        self.k2=0.60;                                    #隐含层偏置项权重
        self.Tg=[0,0];                                   #训练目标
        self.O=[0,0];                                    #网络实际输出    def sigmoid(self,z):        #激活函数        return 1 / (1 + math.exp(-z)) 

    def getLoss(self):        #损失函数        return ((self.O[0] -self.Tg[0])**2+ (self.O[1] - self.Tg[1])**2)/2;    def forwardPropagation(self,input1,input2):        #前向传播
        self.inlayer[0].value = input1;
        self.inlayer[1].value = input2;        for hNNum in range(0,2):             #算出隐含层结点的值
            z = 0;            for iNNum in range(0,2):
                z+=self.inlayer[iNNum].value*self.inlayer[iNNum].W[hNNum];            #加上偏置项
            z+= self.k1;
            self.hidlayer[hNNum].value = self.sigmoid(z);        for oNNum in range(0,2):            #算出输出层结点的值
            z = 0;            for hNNum in range(0,2):
                z += self.hidlayer[hNNum].value* self.hidlayer[hNNum].W[oNNum];
            z += self.k2;
            self.outlayer[oNNum].value = self.sigmoid(z);
            self.O[oNNum] = self.sigmoid(z);    def backPropagation(self,T1,T2):        #反向传播，这里为了公式好看一点多写了一些变量作为中间值        #计算过程用到的公式在博文中已经推导过了，如果代码没看明白请看看博文 
        self.Tg[0] = T1;
        self.Tg[1] = T2;        for iNNum in range(0,2):            #更新输入层权重            for wnum in range(0,2):
                y = self.hidlayer[wnum].value;
                self.inlayer[iNNum].W[wnum] -= self.yita*((self.O[0] - self.Tg[0])*self.O[0] *(1- self.O[0])*\
                    self.hidlayer[wnum].W[0] +(self.O[1] - self.Tg[1])*self.O[1] *(1 - self.O[1])*\
                    self.hidlayer[wnum].W[1])*y*(1- y)*self.inlayer[iNNum].value;        for hNNum in range(0,2):            #更新隐含层权重            for wnum in range(0,2):
                self.hidlayer[hNNum].W[wnum]-= self.yita*(self.O[wnum] - self.Tg[wnum])*self.O[wnum]*\
                    (1- self.O[wnum])*self.hidlayer[hNNum].value;    def printresual(self):        #信息打印
        loss = self.getLoss();
        print("loss",loss);
        print("输出1",self.O[0]);
        print("输出2",self.O[1]);#主程序mnet=net();for n in range(0,20000):
    mnet.forwardPropagation(0.05, 0.1);
    mnet.backPropagation(0.01, 0.99);    if (n%1000==0):
        mnet.printresual();

pytorch的CPU实现

　　用pytorch实现的时候并没有用文章示例中给的参数进行初始化，因为那样很麻烦，而且也并不重要，因此用自带函数初始化了参数。

import timeimport torchimport torch.nn as nnfrom torch.autograd import Variableclass Net(nn.Module):    def __init__(self):        #定义Net的初始化函数，这个函数定义了该神经网络的基本结构
        super(Net, self).__init__() #复制并使用Net的父类的初始化方法，即先运行nn.Module的初始化函数
        self.intohid_layer = nn.Linear(2, 2); #定义输入层到隐含层的连结关系函数
        self.hidtoout_layer = nn.Linear(2, 2);#定义隐含层到输出层的连结关系函数    def forward(self, input):        #定义该神经网络的向前传播函数，该函数必须定义，一旦定义成功，向后传播函数也会自动生成
        x = torch.nn.functional.sigmoid(self.intohid_layer(input))    #输入input在输入层经过经过加权和与激活函数后到达隐含层
        x = torch.nn.functional.sigmoid(self.hidtoout_layer(x))       #类似上面        return x

mnet = Net()
target=Variable(torch.FloatTensor([0.01, 0.99]));   #目标输出input=Variable(torch.FloatTensor([0.05, 0.01]));    #输入loss_fn = torch.nn.MSELoss();                       #损失函数定义，可修改optimizer = torch.optim.SGD(mnet.parameters(), lr=0.5, momentum=0.9);

start = time.time()for t in range(0,5000):
    optimizer.zero_grad();      #清空节点值
    out=mnet(input);            #前向传播
    loss = loss_fn(out,target); #损失计算
    loss.backward();            #后向传播
    optimizer.step();           #更新权值    if (t%1000==0):
        print(out);

end = time.time()
print(end - start)

　　现成的架构实现起来就是简单，代码量呈指数下降，上面的代码运行要8s左右，下面试试看用GPU的要多久。

pytorch的GPU实现

　　看现有的资料pytorch使用GPU非常简单，只需要在数据和模型后面加上“.cuda()”即可。

import timeimport torchimport torch.nn as nnfrom torch.autograd import Variableclass Net(nn.Module):    def __init__(self):        #定义Net的初始化函数，这个函数定义了该神经网络的基本结构
        super(Net, self).__init__() #复制并使用Net的父类的初始化方法，即先运行nn.Module的初始化函数
        self.intohid_layer = nn.Linear(2, 2); #定义输入层到隐含层的连结关系函数
        self.hidtoout_layer = nn.Linear(2, 2);#定义隐含层到输出层的连结关系函数    def forward(self, input):        #定义该神经网络的向前传播函数，该函数必须定义，一旦定义成功，向后传播函数也会自动生成
        x = torch.nn.functional.sigmoid(self.intohid_layer(input))    #输入input在输入层经过经过加权和与激活函数后到达隐含层
        x = torch.nn.functional.sigmoid(self.hidtoout_layer(x))       #类似上面        return x

mnet = Net().cuda()
target=Variable(torch.cuda.FloatTensor([0.01, 0.99]));   #目标输出input=Variable(torch.cuda.FloatTensor([0.05, 0.01]));    #输入loss_fn = torch.nn.MSELoss();                            #损失函数定义，可修改optimizer = torch.optim.SGD(mnet.parameters(), lr=0.5, momentum=0.9);

start = time.time()for t in range(0,5000):
    optimizer.zero_grad();      #清空节点值
    out=mnet(input);            #前向传播
    loss = loss_fn(out,target); #损失计算
    loss.backward();            #后向传播
    optimizer.step();           #更新权值print(out.cpu());
end = time.time()
print(end - start)