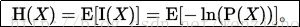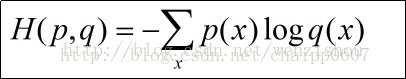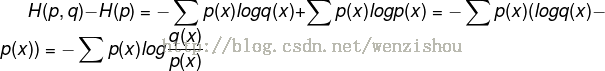为什么交叉熵能作为损失函数及其弥补了平方差损失什么缺陷
在很多二分类问题中,特别是正负样本不均衡的分类问题中,常使用交叉熵作为loss对模型的参数求梯度进行更新,那为何交叉熵能作为损失函数呢,我也是带着这个问题去找解析的。
以下仅为个人理解,如有不当地方,请读到的看客能指出。
我们都知道,各种机器学习模型都是模拟输入的分布,使得模型输出的分布尽量与训练数据一致,最直观的就是MSE(均方误差,Mean squared deviation), 直接就是输出与输入的差值平方,尽量保证输入与输出相同。这种loss我们都能理解。
以下按照(1)熵的定义(2)交叉熵的定义 (3) 交叉熵的由来 (4)交叉熵作为loss的优势 作为主线来一步步理清思路。
(1)熵的定义 各种熵的名称均来自信息论领域,这方面的背景就不介绍了,随便就能找到很多。
根据维基的定义,熵的定义如下:熵是接收的每条消息中包含的信息的平均量,又被称为信息熵、信源熵、平均自信息量。直白地解释就是信息中含的信息量的大小,其定义如下:
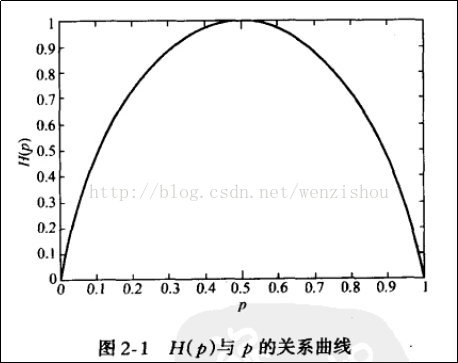
其曲线如下所示:
可以看出,一个事件的发生的概率离0.5越近,其熵就越大,概率为0或1就是确定性事件,不能为我们带信息量。也可以看作是一件事我们越难猜测是否会发生,它的信息熵就越大
(2)交叉熵的定义 交叉熵的公式定义如下:
其中p(x)在机器学习中为样本label,q(x)为模型的预估,分别代表训练样本和模型的分布,如果只是根据这个公式,是看不出来什么的,暂且放下,继续往下看
(3)交叉熵的由来 将上面的交叉熵的公式减去一个固定的值(H(p), 训练样本的熵,训练样本定,该值即为固定值),即训练样本分布p(x)的熵,可得如下:
最后得到的为相对熵或KL散度(Kullback-Leibler divergence), 亦可称为KL距离,是用于评判两个分布的差异程序,看到这里,应该明白为何交叉熵为何能作为loss了。即可以使得模型输出的分布尽量与训练样本的分布一致
(4)交叉熵作为loss的优势 模型训练的loss有很多,交叉熵作为loss有很多应用场景,其最大的好处我认为是可以避免梯度消散,因为一般我们使用平方差作为损失函数,(
那我们再讨论一下,平方差为什么会梯度弥散,而交叉熵不会:
因为y求导为y(y-1)所以趋近于0或1时上述倒数趋近于零,梯度弥散。
与sigmoid导数无关,从而避免了梯度弥散。