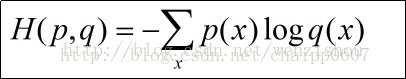我们简单介绍了相对熵的概念，知道了相对熵可以用来表达真实事件和理论拟合出来的事件之间的差异。

相对熵的公式如下：
$$
D _ { K L } ( p | q ) = \sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log p \left( x _ { i } \right)-\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)
$$
可以看到前面一项是真实事件的信息熵取反，我们可以直接写成
$$
D _ { K L } ( p | q ) = -H(p)-\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)
$$
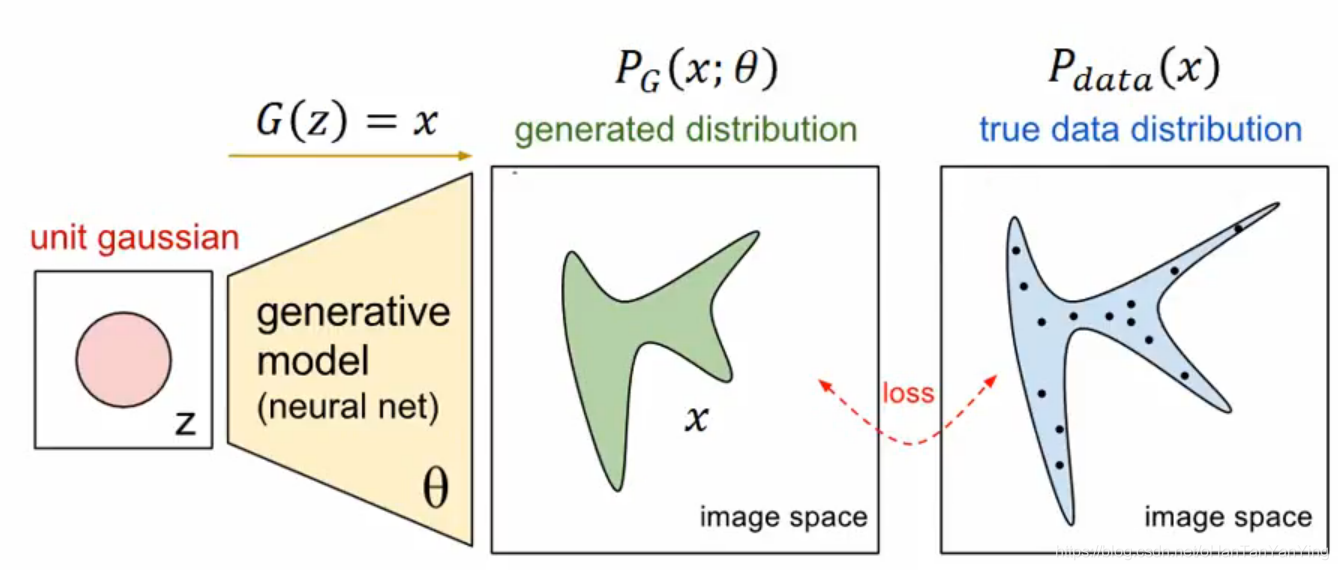
在神经网络训练中，我们要训练的是
$$
q ( x _ { i })
$$
使得其与真实事件的分布越接近越好，也就是说在神经网络的训练中，相对熵会变的部分只有后面的部分，我们希望它越小越好，而前面的那部分是不变的。因此我们可以把后面的部分单独取出来，那部分就是交叉熵，写作：
$$
H(p，q) = -\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)
$$
这就是我们经常在神经网络训练中看到的交叉熵损失函数。如果要了解它的内涵，要回头去看相对熵。