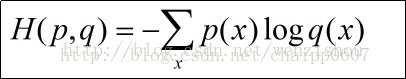香农信息量
如果是连续型随机变量的情况,设p为随机变量X的概率分布,即p(x)为随机变量X在X=x处的概率密度函数值,则随机变量X在X=x处的香农信息量定义为:-
$$
log_2p(x)=log_2\frac{1}{p(x)}
$$
这时香农信息量的单位为比特。(如果非连续型随机变量,则为某一具体随机事件的概率,其他的同上)
香农信息量用于刻画消除随机变量在处的不确定性所需的信息量的大小。
上面是香农信息量的完整而严谨的表达,基本上读完就只剩下一个问题,为什么是这个式子?为了方便理解我们先看一下香农信息量在数据压缩应用的一般流程。
假设我们有一段数据长下面这样:aaBaaaVaaaaa
可以算出三个字母出现的概率分别为:
$$
a:\frac{10}{12},B:\frac{1}{12},V:\frac{1}{12}
$$
香农信息量为:a:0.263,B:3.585,V:3.585
也就是说如果我们要用比特来表述这几个字母,分别需要0.263,3.585,3.585个这样的比特。当然,由于比特是整数的,因此应该向上取整,变为1,4,4个比特。
这个时候我们就可以按照这个指导对字母进行编码,比如把a编码为”00”,把B编码为”10001000”,V编码为”10011001”,然后用编码替换掉字母来完成压缩编码,数据压缩结果为:001000000100100000。
上面例子看起来有点不合理,因为如果我们去搞,我们会编码出不一样的东西,如a编码为”00”,B编码为”1010”,V编码为”1111”,因此可以把数据压缩的更小。那么问题出现在哪呢?
出现在这里的B和V这两个字母只用两个比特进行编码对于他们自身而言并不是充分的。在另外一个压缩的例子中,可以一下子就看出来:abBcdeVfhgim
上面的每一个字母出现的概率都为
$$
\frac{1}{12}
$$
,假设我们还是以两个比特去编码B和V,那么就无法完全区分出12个字母。而如果是4个比特,便有16种可能性,可以足够区分这12个字母。
现在回过头来看香农信息量的公式,它正是告诉我们,如果已经知道一个事件出现的概率,至少需要多少的比特数才能完整描绘这个事件(无论外部其他事件的概率怎么变化),其中为底的2就是比特的两种可能性,而因为二分是一个除的关系,因此自变量是概率分之一而不是概率本身。
感性的看,如果我们知道a出现的概率为
$$
\frac{5}{6}
$$
,那么用比特中的”0”状态来表述它是完全合理的,因为其他事件的概率总和只有
$$
\frac{1}{6}
$$
,但我们给这
$$
\frac{1}{6}
$$
空出了比特的”1”这
$$
\frac{1}{2}
$$
的空间来表达他们,是完全足够的。